VECTOR WORD PROBLEMS AND ANSWERS

Problem 1 :

If G is the centroid of a triangle ABC, prove that GA vector + GB vector  + GC vector = 0.

Answer :

From the given information, let us draw a rough diagram.

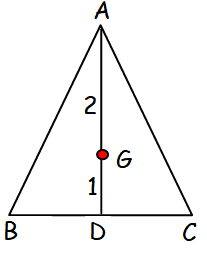
Centroid of the triangle divides in the ratio 2 : 1.

OA vector  =  a vector

OB vector =  b vector

OC vector  =  c vector

OG vector  =   [m (OD vector) + n (OA vector)] / (m + n)

OG vector  =   [2(OD vector) + 1(OA vector)] / (2+1)

OG vector  =   [2(OD vector) + 1(OA vector)] / 3  ---(1)

D is the midpoint of the side BC.

OD vector  =  (OB vector + OC vector) /2

By applying the value of OD in (1), we get

OG vector  =   (OB vector + OC vector + OA vector)/3

3OG vector  =  OA vector + OB vector + OC vector

(OA-OG) vector + (OB-OG) Vector + (OC-OG) vector  =  0

GA vector + GB vector + GC vector  =  0

Problem 2 :

Let A, B, and C be the vertices of a triangle. Let D,E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that AD vector + BE vector + CF vector  = 0.

Answer :

Let us draw a picture using the given information.

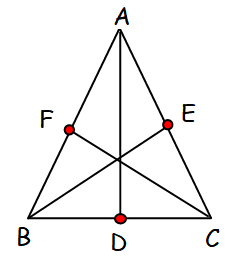
OA vector  =  a vector

OB vector  =  b vector

OC vector  =  c vector

OD = (OB + OC)/2  =  (b + c) / 2

OE = (OA + OC)/2  =  (a + c) / 2

OF = (OA + OB)/2  =  (a + b) / 2

AD vector :

AD vector  =  (OD - OA) vector  ----(1)

By applying OD in (1), we get

  =  ((b + c)/2) - a

  =  (b + c - 2a)/2

BE vector :

BE vector  =  (OE - OB) vector  ----(2)

By applying OE in (2), we get

  =  ((a + c)/2) - b

  =  (a + c - 2b)/2

CF vector :

CF vector  =  (OF - OC) vector  ----(3)

By applying OF in (3), we get

  =  ((a + b)/2) - c

  =  (a + b - 2c)/2

AD vector + BE vector + CF vector  = 0

  =  [(b + c - 2a) + (a + c - 2b) +  (a + b - 2c)]/2

  =  0

Hence it is proved.

Problem 3 :

If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then prove that AB vector + AD vector + CB vector + CD vector = 4EF vector.

Answer :

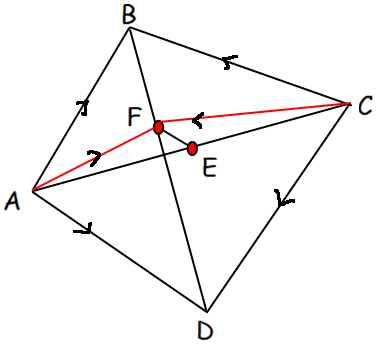
Since F is the midpoint of the side BD, 

AF vector  =  (AB vector + AD vector) /2

2AF vector  =  AB vector + AD vector  ----(1)

CF vector  =  (CB vector + CD vector) /2

2CF vector  =  CB vector + CD vector  ----(2)

(1) + (2)

2AF vector + 2CF vector 

  =  (AB vector + AD vector) + (CB vector + CD vector)

2(AF vector + CF vector)

  =  (AB vector + AD vector) + (CB vector + CD vector)

Instead of AF + CF, we may write 2EF (using midpoint formula vice versa)

AB vector + AD vector + CB vector + CD vector  =  4  EF

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.