USING UNIT RATES TO SOLVE PROPORTIONS

A unit rate describes how many units of the first type of quantity corresponds to one unit of the second type of quantity.

Examples :

30 miles per hour

$15 per unit

A proportion is an equation that states that two ratios or rates are equivalent.

Examples :

1/3 and 2/6 are equivalent ratios

1/3  =  2/6 is a proportion

Here, we are going to see how unit rates can be used to solve proportions.

Solved Problems

Problem 1 :

The distance Ali runs in 40 minutes is 3 miles. At this rate, how far can he run in 60 minutes?

Solution :

Let A be the number of miles that he can run in 60 minutes.

From the given information, we can write the following proportion.

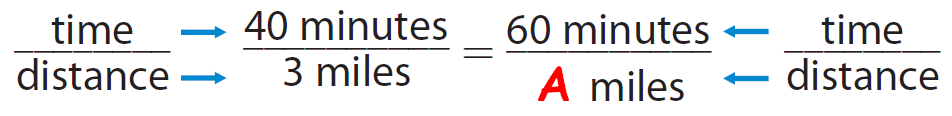
Since, we want to find the number of miles covered in 60 minutes, we have to convert the first quantity of the ratio

40 minutes / 3 miles

into 60 minutes.

But 60 is not a multiple of 40. So, let us convert the above ratio into unit rate.

That is, number of miles covered in 1 minute.

Then, we can convert the first quantity into 60 minutes using multiplication.

The picture given below clearly illustrates this.

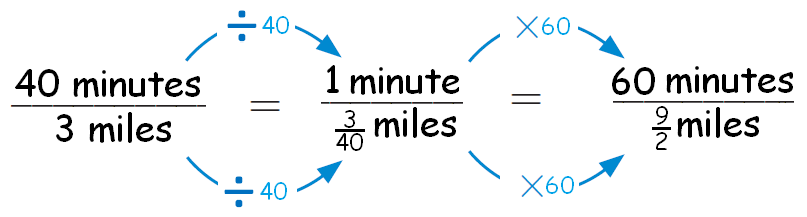
At this rate, Ali can run 9/2 miles, or 4 1/2 miles, in 60 minutes.

Problem 2 :

Ms. Reynolds has a system of 10 sprinklers that water her entire lawn. The sprinklers run one at a time, and each runs for the same amount of time. The first 4 sprinklers run for a total of 50 minutes. How long does it take to water her entire lawn?

Solution :

Let T be the time takes to water the entire lawn.

From the given information, we can write the following proportion.

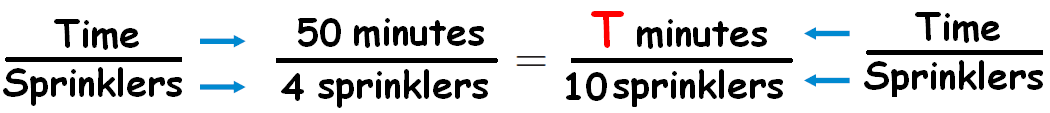
We want to find the time taken to water the entire lawn and 10 sprinklers needed to water the entire lawn.

So, we have to convert the second quantity of the ratio

50 minutes/4 sprinklers

into 10 sprinklers.

But 10 is not a multiple of 4. So, let us convert the above ratio into unit rate.

That is, number of minutes taken for each sprinkler.

Then, we can convert the second quantity into 10 sprinklers using multiplication.

The picture given below clearly illustrates this.

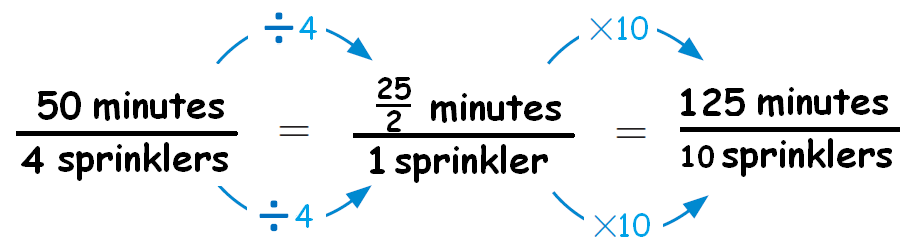
So, it takes 125 minutes or 2 hours 5 minutes to water her entire lawn.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.