USING THE DISTANCE FORMULA

The distance formula is a formula for computing the distance between two points. 

Let A(x₁, y₁) and B(x₂, y₂) be the two points in a coordinate plane as shown below.  

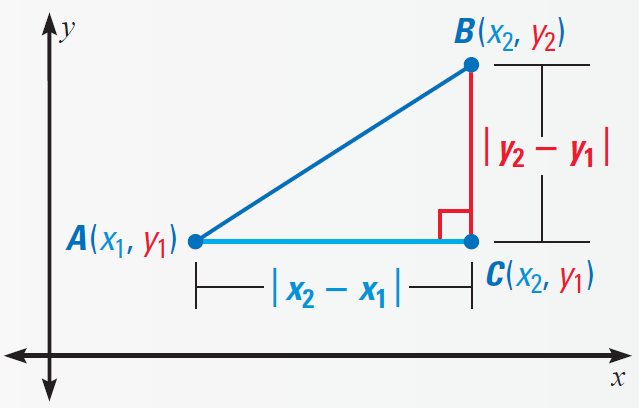
Then, the distance between A and B is 

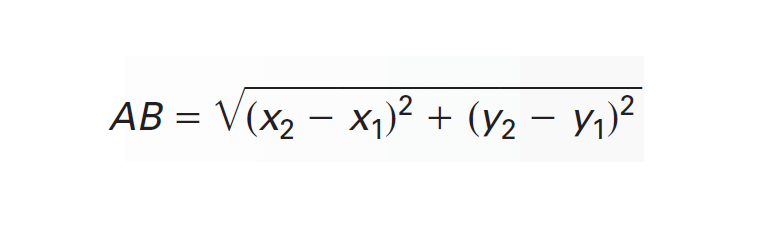
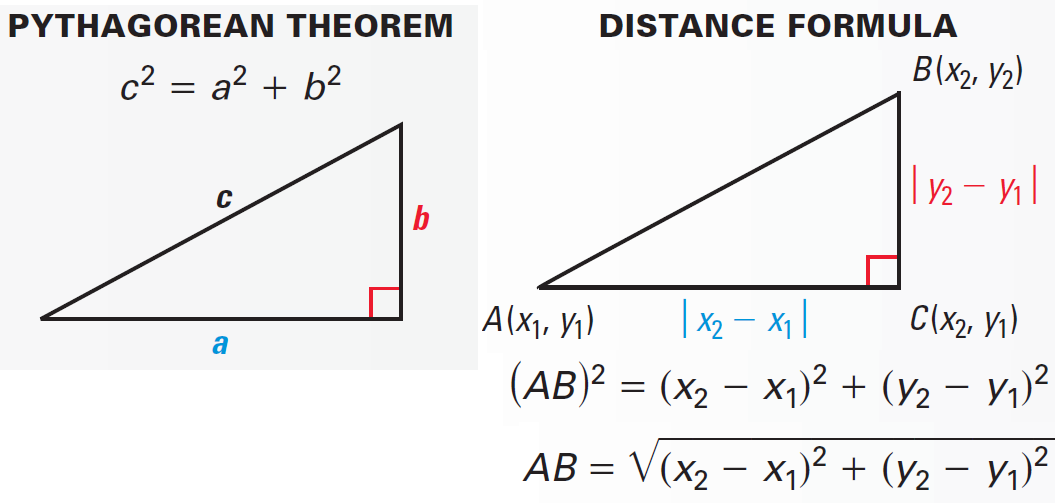
The distance formula is based on Pythagorean Theorem. It has been explained below.

Solved Problems

Problem 1 :

Find the lengths of the segments AB, AC and AD. Say whether any of the segments have the same length. 

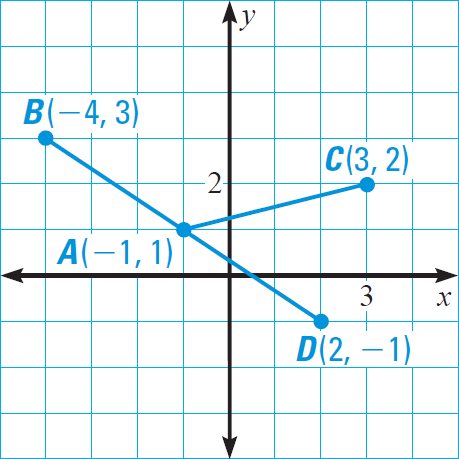
Use the distance formula to find the length of each segment. 

Length of AB :

(x₁, y₁)  =  A(-1, 1)

(x₂, y₂)  =  B(-4, 3)

Then, we have

AB  =  √[(-4 + 1)² + (3 - 1)²]

AB  =  √[(-3)² + (2)²]

AB  =  √[9 + 4]

AB  =  √13

Length of AC :

(x₁, y₁)  =  A(-1, 1)

(x₂, y₂)   =  C(3, 2)

Then, we have

AC  =  √[(3 + 1)² + (2 - 1)²]

AC  =  √[(4)² + (1)²]

AC  =  √[16 + 1]

AC  =  √17

Length of AD :

(x₁, y₁)  =  A(-1, 1)

(x₂, y₂)  =  D(2, -1)

Then, we have

AD  =  √[(2 + 1)² + (-1 - 1)²]

AD  =  √[(3)² + (-2)²]

AD  =  √[9 + 4]

AD  =  √13

So, AB and AD have the same lengths, but AC has different length.

Note : 

Segments that have the same length are called congruent segments. For instance, in the above example, segments AB and AD are congruent, because each has a length of √13 units. 

There is a special symbol, ≅ for indicating congruence. 

So, we have

AB ≅ AD

Problem 2 :

On the map shown below, the city blocks are 340 feet apart east-west and 480 feet apart north-south. 

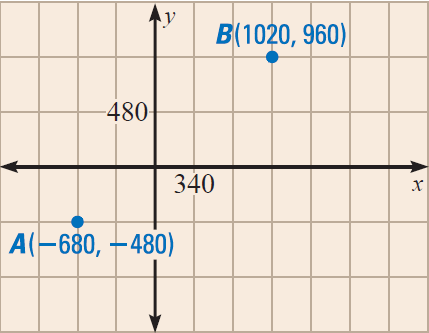
(i) Find the walking distance between A and B. 

(ii) What would the distance be if a diagonal street existed between the two points ? 

Solution : 

Solution (i) :

To walk from A to B, we would have to walk five blocks east and three blocks north.  

5 blocks ⋅ 340 feet/block  =  1700 feet

3 blocks ⋅ 480 feet/block  =  1440 feet

So, the walking distance is 

1700 + 1440  =  3140 feet

Solution (ii) :

To find the diagonal distance between A and B, use the distance formula. 

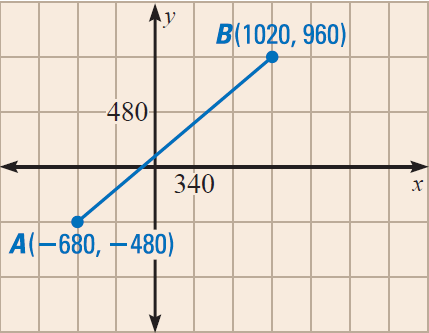
(x₁, y₁)  =  A(-680, -480)

(x₂, y₂)  =  B(1020, 960)

Then, we have

AB  =  √[(1020 + 680)² + (960 + 480)²]

AB  =  √[(1700)² + (1440)²]

AB  =  √4,963,600

AB  ≈  2228 feet

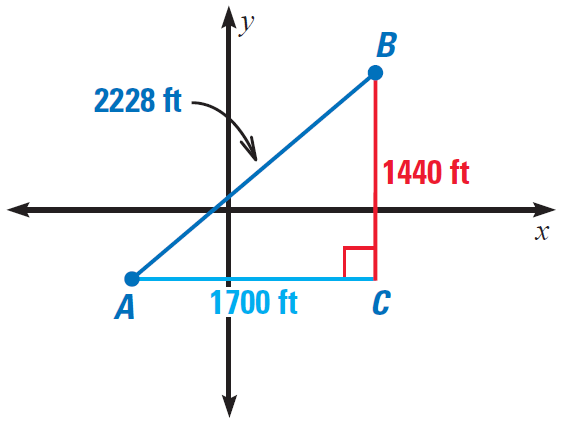
So, the diagonal distance would be about 2228 feet, that is 912 feet less than walking distance.

It has been illustrated in the picture given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.