USING THE CONVERSE OF THE PYTHAGOREAN THEOREM
Converse of the Pythagorean Theorem
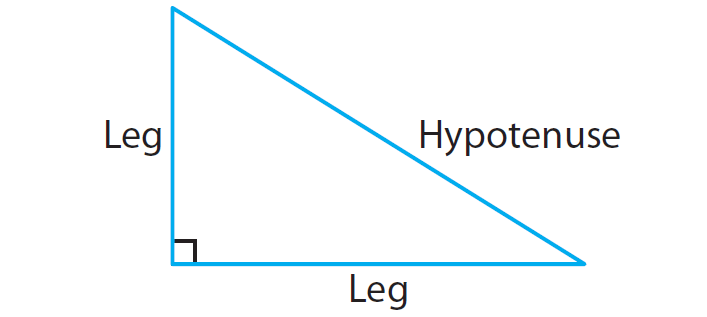
The Pythagorean Theorem states that if a triangle is a right triangle, then, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
That is, if a and b are legs and c is the hypotenuse, then
a2 + b2 = c2
The converse of the Pythagorean Theorem states that if a2 + b2 = c2, then the triangle is a right triangle.
Using the Converse of the Pythagorean Theorem
Example 1 :
Tanya is buying edging for a triangular flower garden she plans to build in her backyard. If the lengths of the three pieces of edging that she purchases are 13 feet, 10 feet, and 7 feet, will the flower garden be in the shape of a right triangle ?
Solution :
Step 1 :
Let a = 10, b = 7, and c = 13.
(Always assume the longest side as 'c')
Step 2 :
Find the value of a2 + b2.
a2 + b2 = 102 + 72
a2 + b2 = 100 + 49
a2 + b2 = 149 -----(1)
Step 3 :
Find the value of c2.
c2 = 132
c2 = 169 -----(2)
Step 4 :
From (1) and (2), we get
a2 + b2 ≠ c2
By the converse of Pythagorean theorem, the triangle with the side lengths 13 feet, 10 feet, and 7 feet is not a right triangle.
So, the garden is not in the shape of a right triangle.
Example 2 :
A blueprint for a new triangular playground shows that the sides measure 480 ft, 140 ft, and 500 ft. Is the playground in the shape of a right triangle ? Explain.
Solution :
Step 1 :
Let a = 480, b = 140, and c = 500.
(Always assume the longest side as 'c')
Step 2 :
Find the value of a2 + b2.
a2 + b2 = 4802 + 1402
a2 + b2 = 230,400 + 19,600
a2 + b2 = 250,0000 -----(1)
Step 3 :
Find the value of c2.
c2 = 5002
c2 = 250,000 -----(2)
Step 4 :
From (1) and (2), we get
a2 + b2 = c2
By the converse of Pythagorean theorem, the triangle with the side lengths 480 ft, 140 ft, and 500 ft is a right triangle.
So, the the playground is in the shape of a right triangle.
Example 3 :
A triangular piece of glass has sides that measure 18 in., 19 in., and 25 in. Is the piece of glass in the shape of a right triangle ? Explain.
Solution :
Step 1 :
Let a = 18, b = 19, and c = 25.
(Always assume the longest side as 'c')
Step 2 :
Find the value of a2 + b2.
a2 + b2 = 182 + 192
a2 + b2 = 324 + 361
a2 + b2 = 685 -----(1)
Step 3 :
Find the value of c².
c2 = 252
c2 = 625 -----(2)
Step 4 :
From (1) and (2), we get
a2 + b2 ≠ c2
By the converse of Pythagorean theorem, the triangle with the side lengths 18 in., 19 in., and 25 in. is not a right triangle.
So, the piece of glass is not in the shape of a right triangle.
Example 4 :
A corner of a fenced yard forms a right angle. Can we place a 12 ft long board across the corner to form a right triangle for which the leg lengths are whole numbers ? Explain.
Solution :
Step 1 :
Let a and b be the legs of the triangle.
Step 2 :
Draw an appropriate diagram for the given information.
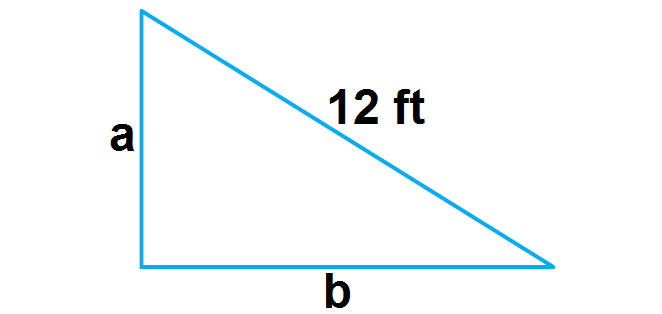
Step 3 :
To form a right triangle, the legs a and b and the length of the board 12 ft must satisfy the converse of the Pythagorean theorem. That is
a2 + b2 = 122
a2 + b2 = 144
But, there are no pairs of whole numbers whose squares add up to 122 = 144.
So, we can not place a 12 foot long board across the corner to form a right triangle for which the leg lengths are whole numbers.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 158)
May 06, 25 11:00 AM
Digital SAT Math Problems and Solutions (Part - 158) -
Digital SAT Math Problems and Solutions (Part - 157)
May 05, 25 10:57 AM
Digital SAT Math Problems and Solutions (Part - 157) -
AP Calculus AB Problems with Solutions (Part - 21)
May 04, 25 11:49 PM
AP Calculus AB Problems with Solutions (Part - 21)