USING TABLES TO COMPARE RATIOS

Example 1 : 

Anna’s recipe for lemonade calls for 2 cups of lemonade concentrate and 3 cups of water. Bailey’s recipe calls for 3 cups of lemonade concentrate and 5 cups of water. Whose recipe makes stronger lemonade? How do you know ?

Solution :

Anna’s recipe :

2 cups of lemonade and 3 cups of water.

So, the ratio is 2 : 3.

Let us write equivalent ratios to the ratio 2 : 3.

Bailey’s recipe :

3 cups of lemonade and 5 cups of water.

So, the ratio is 3 : 5.

Let us write equivalent ratios to the ratio 3 : 5.

Find two columns, one in each table, in which the amount of water is the same. Circle those two columns.

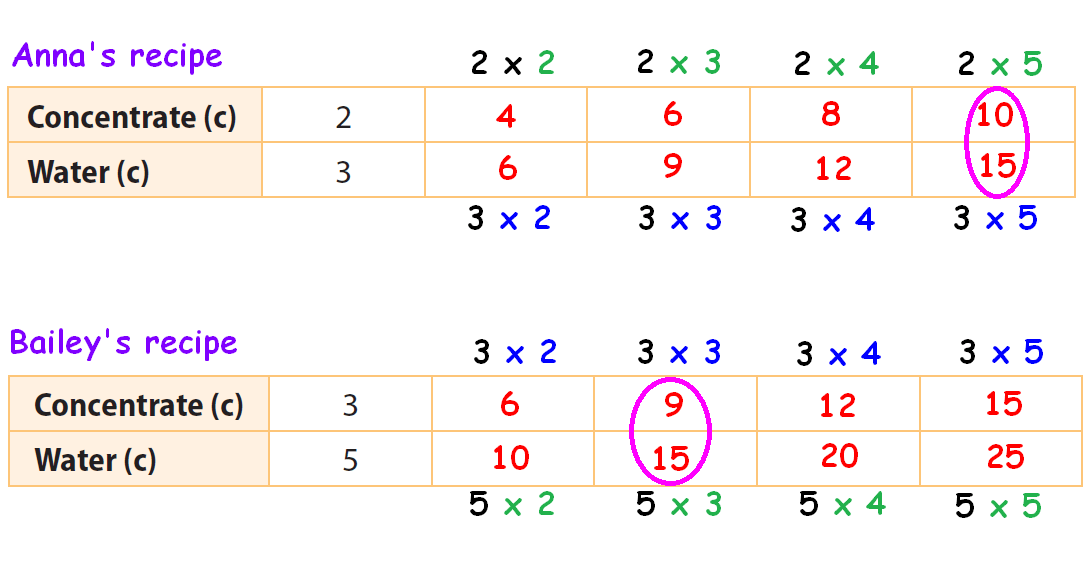
From the circled columns, we get two ratios. 

They are, 

10 : 15 and 9 : 15

In these two ratios, the second quantity (water) is same. 

So, we have to compare the first quantity (Lemonade).

The first quantity (10) in the first ratio is more than the first quantity (9) in the second ratio. 

When the quantity of water is same (15) in both recipes, Anna's recipe has more quantity of lemonade concentrate.

Therefore, Anna's recipe has stronger lemonade. 

Example 2 : 

Find which ratio is greater :

2 1/3 : 3 1/3 and 3.6 : 4.8

Solution :

If we want to compare two ratios using table, both the terms of the ratio must be integers. 

Let us convert the terms of the first ratio into integers. 

2 1/3  :  3  1/3  =  (7/3) : (10/3)

2 1/3  :  3  1/3  =  7 : 10 ------> multiplied by 3 

Let us write equivalent ratios to the ratio 7 : 10

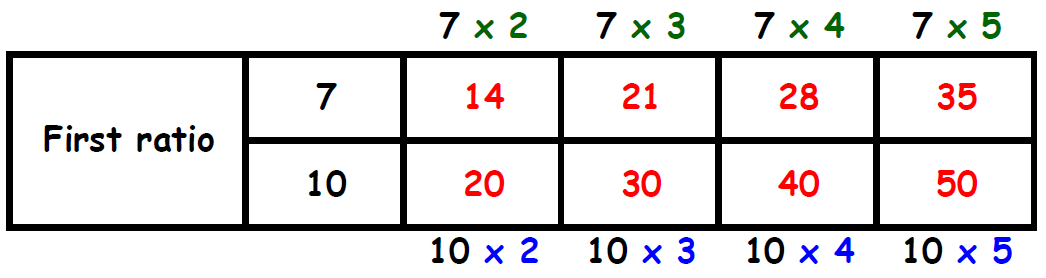
Let us convert the terms of the second ratio into integers. 

3.6 : 4.8  =  36 : 48 ------> multiplied by 10 

3.6 : 4.8  =  3 : 4 ------> divided by 12 

Let us write equivalent ratios to the ratio 3 : 4

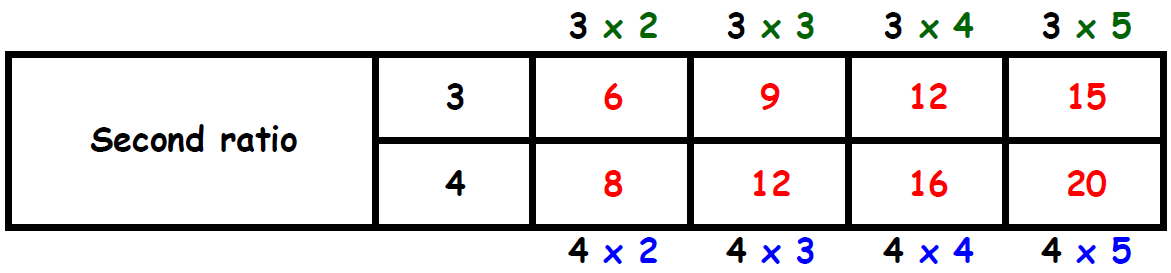
Find two columns, one in each table, in which the the second term is same. Circle those two columns.

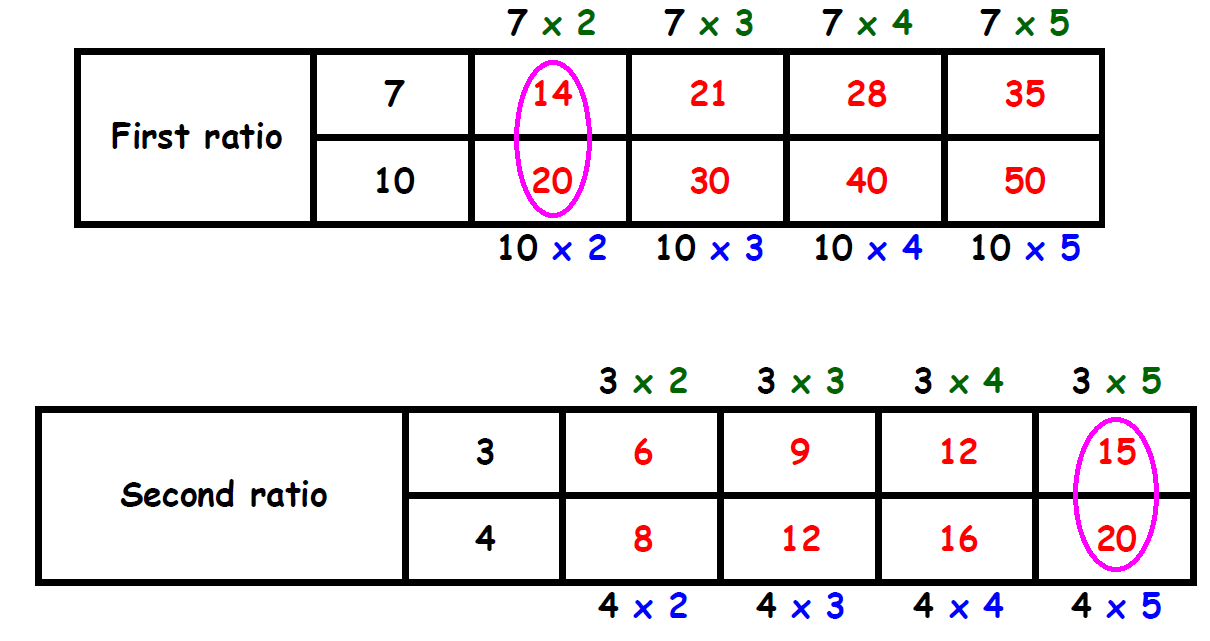
From the circled columns, we get two ratios. 

They are, 

14 : 20 and 15 : 20

In these two ratios, the second term is same. 

So, we have to compare the first terms 14 and 15.

The first term in the second ratio (15) is more than the first term in the first ratio (14).

Therefore, the second ratio is greater than the first ratio.

That is, 3.6 : 4.8 is greater than 2 1/3 : 3 1/3.

Example 3 : 

You answer 24 out of 30 questions correctly on a quiz. Your friend answers 35 out of 40 questions correctly on a different quiz. Who has the better score?

Solution :

Ratio on your quiz :

24 : 30

Ratio of your friend's quiz :

35 : 40

Comparing these two ratios,

LCM (30, 40) = 120

(24/30)⋅(4/4) ==> 96/120

(35/40)⋅(3/3) ==> 105/120

96/120 < 105/120

24/30 < 35/40

So, your friend has scored better.

Example 4 : 

The table shows the number of hits and at bats for four softball players.

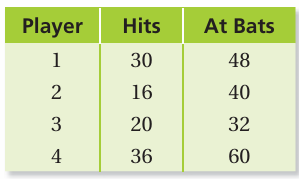
a. Write each player’s batting average as a ratio of hits to at bats.

b. Did the player with the most hits have the best batting average? Explain

Solution :

a)  Ratio between hits to at bats :

b) 

• Average of player 1 = 0.625
• Average of player 2 = 0.4
• Average of player 3 = 0.625
• Average of player 4 = 0.6

Player 4 has maximum hit, but his average is not high.

Example 5 : 

There are 12 boys and 10 girls in your gym class. If 6 boys joined the class, how many girls would need to join for the ratio to remain the same?

Solution :

Ratio between boys to girls = 12 : 10

= 6 : 5

When 6 boys are joined, let x be the number of girls are joining.

(12 + 6) : (10 + x) = 6 : 5

18 : (10 + x) = 6 : 5

18/(10 + x) = 6/5

5(18) = 6(10 + x)

90 = 60 + 6x

90 - 60 = 6x

6x = 30

x = 30/6

x = 5

So, new number of girls to be added is 5 to remain the ratio same.

Example 6 : 

Your neighbor pays you $17 for every 2 hours you work. You work for 8 hours on Saturday. How much does your neighbor owe you?

Solution :

Ratio between the number of hours working and the amount what we receive.

= 2 : 17

Let x be the amount received when working for 8 hours.

2 : 17 = 8 : x

2/17 = 8/x

2x = 17(8)

x = 17(4)

= 68

So, for working 8 hours, i should get $68.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.