USING SIMILAR TRIANGLES TO MEASURE HEIGHT

Because corresponding angles are congruent and corresponding sides are proportional in similar triangles, we can use similar triangles to measure height in real-world problems.

Examples

Example 1 : 

While playing tennis, David is 12 meters from the net, which is 0.9 meter high. He needs to hit the ball so that it just clears the net and lands 6 meters beyond the base of the net. At what height should Matt hit the tennis ball ?

Solution :

Step 1 :

Draw an appropriate diagram to the given information

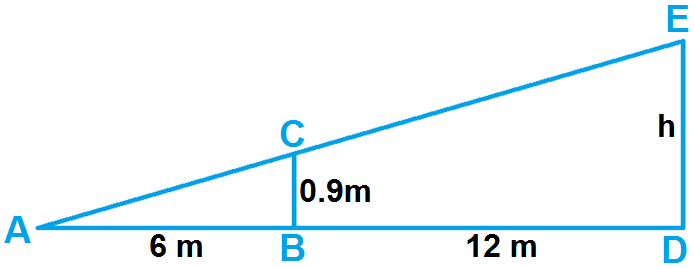
In the above diagram, 

BC  =  Height of the net

DE  =  Height of ball when hit

A  =  Point at where the ball lands

Step 2 : 

Let us compare two corresponding angles of triangles ABC and ADE. 

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Step 3 : 

Since the triangles ABC and ADE are similar triangles,  corresponding side lengths are proportional.

So, we have

AD / DB  =  DE / BC

(AB + BD) / DB  =  DE / BC

Substitute the lengths from the figure.

(6 + 12) / 6  =  h / 0.9

18 / 6  =  h / 0.9

3  =  h / 0.9

Multiply both sides by 0.9

3 ⋅ 0.9  =  (h/0.9) ⋅ 9

2.7  =  h

So, David should hit the ball at a height of 2.7 meters.

Example 2 : 

The lower cable meets the tree at a height of 6 feet and extends out 16 feet from the base of the tree. If the triangles are similar, how tall is the tree ?

Solution :

Step 1 :

Draw an appropriate diagram to the given information

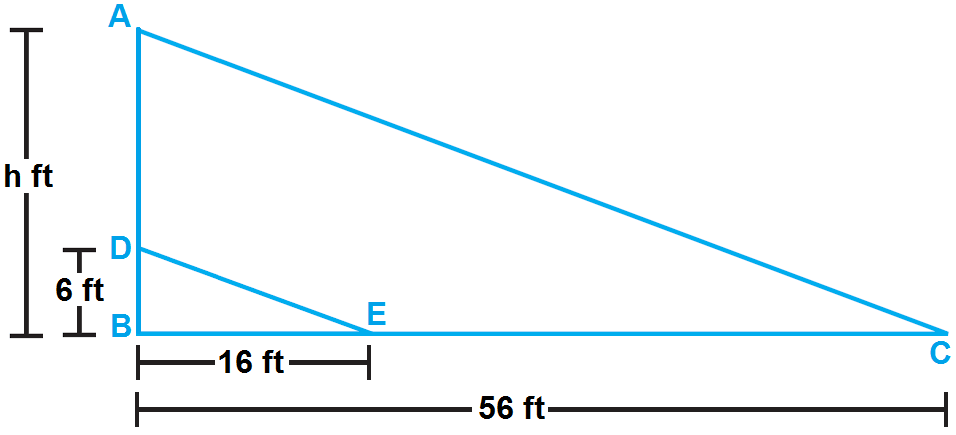
In the above diagram, 

AB  =  Height of the tree

CD  =  Height at where the lower cable meets the tree

Step 2 : 

Since the triangles ABC and DBE are similar triangles,  corresponding side lengths are proportional.

So, we have

AB / DB  =  BC / BE

Substitute the lengths from the figure.

h / 6  =  56 / 16

h / 6  =  7 / 2

Multiply both sides by 6.

(h/6) ⋅ 6  =  (7/2) ⋅ 6

h  =  21

So, the height of the tree is 21 ft. 

Example 3 : 

Jose is building a wheelchair ramp that is 24 feet long and 2 feet high. She needs to install a vertical support piece 8 feet from the end of the ramp. What is the height of the support piece in inches ?

Solution :

Step 1 :

Draw an appropriate diagram to the given information

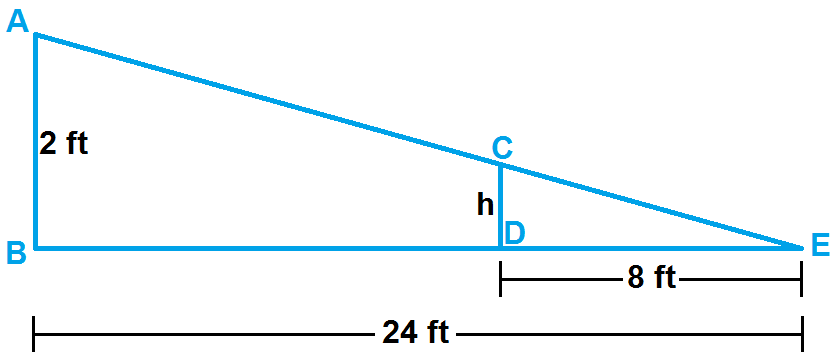
In the above diagram, 

AB  =  Height of the chair

CD  =  Height of the support piece

E  =  End of the ramp

Step 2 : 

Let us compare two corresponding angles of triangle ABE and CDE. 

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Step 3 : 

Since the triangles ABE and ADE are similar triangles,  corresponding side lengths are proportional.

So, we have

DE / BE  =  CD / AB

Substitute the lengths from the figure.

8 / 24  =  h / 2

1 / 3  =  h / 2

Multiply both sides by 2.

(1/3) ⋅ 2  =  (h/2) ⋅ 2

2/3 ft  =  h

or 

h  =  2/3 ft

Step 4 : 

Convert feet into inches.

Since 1 ft = 12 inches, we have to multiply by 12 to convert ft into inches.   

h  =  2/3 ft ----> h  =  (2/3) ⋅ 12 inches

h  =  8 inches

So, the height of the support piece is 8 inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.