USING RATIOS AND RATES TO SOLVE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
There are two alloys A and B, both are made up of gold and copper. The ratio between gold and copper in each alloy is given below.
Alloy A (G : C)----> 2 1/3 : 3 1/3
Alloy B (G : C) ----> 3.6 : 4.8
In which alloy do we have more gold ?
Solution :
To know the alloy in which we have more gold, we have to compare the given two ratios.
To compare two ratios, both the terms of the ratio must be integers.
Let us convert the terms of the first ratio into integers.
2 1/3 : 3 1/3 = (7/3) : (10/3)
2 1/3 : 3 1/3 = 7 : 10 ------> multiplied by 3
Let us write equivalent ratios to the ratio 7 : 10.
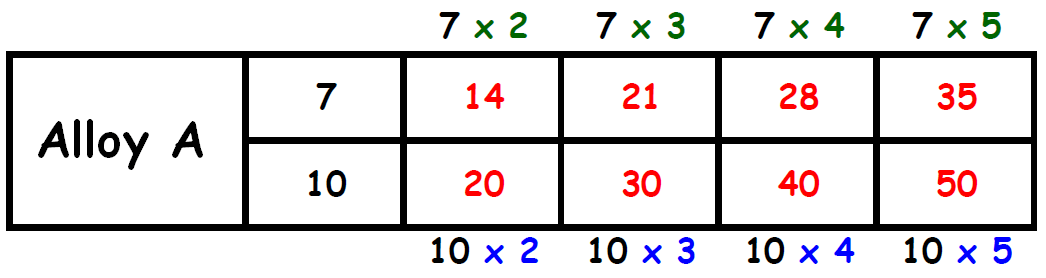
Let us convert the terms of the second ratio into integers.
3.6 : 4.8 = 36 : 48 ------> multiplied by 10
3.6 : 4.8 = 3 : 4 ------> divided by 12
Let us write equivalent ratios to the ratio 3 : 4.
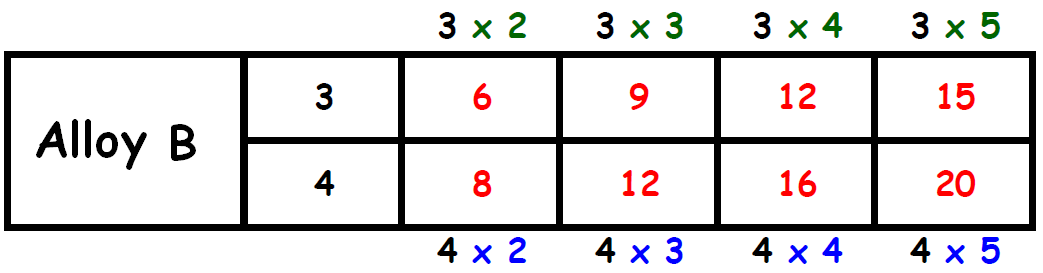
Find two columns, one in each table, in which the the second term is same. Circle those two columns.
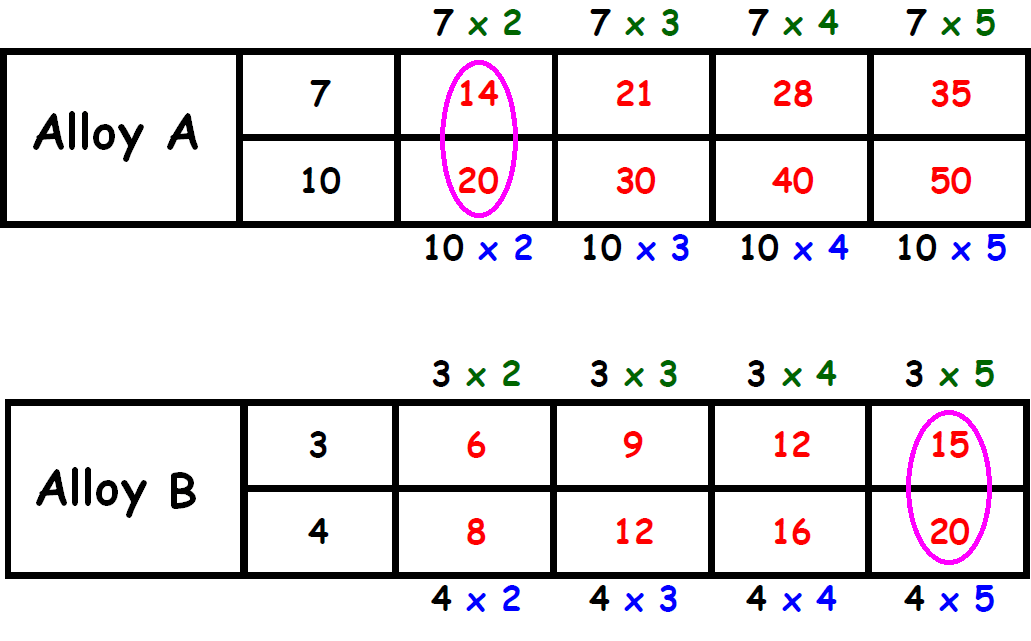
From the circled columns, we get two ratios.
They are,
14 : 20 and 15 : 20
In these two ratios, the second quantity (copper) is same.
So, we have to compare the first quantity (gold).
The first quantity (15) in the second ratio is more than the first quantity (14) in the first ratio.
When the quantity of copper is same (20) in both the alloys, Alloy A has more quantity of gold.
Therefore, we have more gold in alloy A.
Problem 2 :
Anna’s recipe for lemonade calls for 2 cups of lemonade concentrate and 3 cups of water. Bailey’s recipe calls for 3 cups of lemonade concentrate and 5 cups of water. Whose recipe makes stronger lemonade? How do you know ?
Solution :
Anna’s recipe :
2 cups of lemonade and 3 cups of water.
So, the ratio is 2 : 3.
Let us write equivalent ratios to the ratio 2 : 3.

Bailey’s recipe :
3 cups of lemonade and 5 cups of water.
So, the ratio is 3 : 5.
Let us write equivalent ratios to the ratio 3 : 5.

Find two columns, one in each table, in which the amount of water is the same. Circle those two columns.
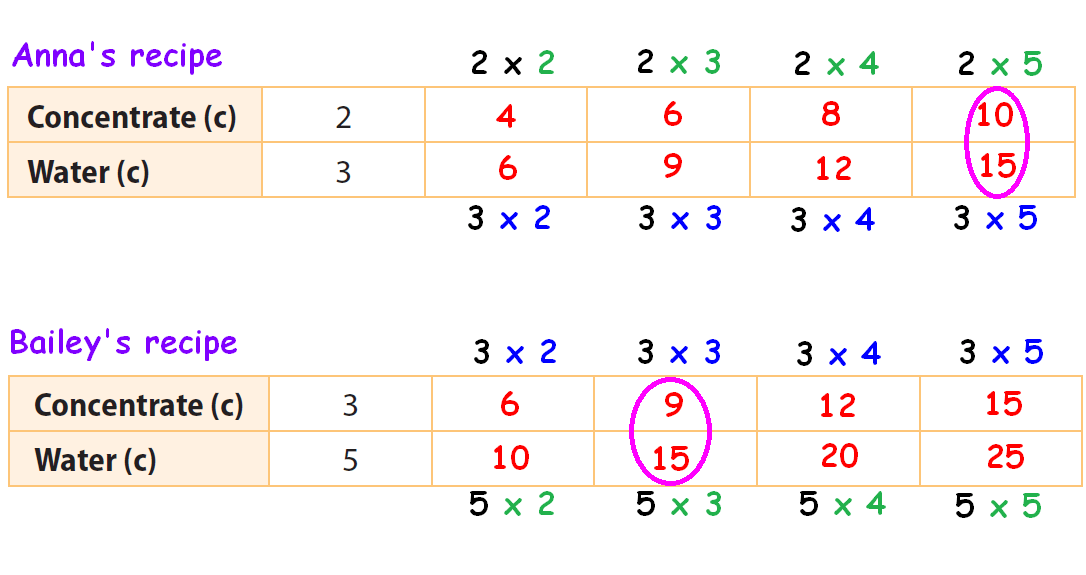
From the circled columns, we get two ratios.
They are,
10 : 15 and 9 : 15
In these two ratios, the second quantity (water) is same.
So, we have to compare the first quantity (Lemonade).
The first quantity (10) in the first ratio is more than the first quantity (9) in the second ratio.
When the amount of water is same (15) in both recipes, Anna's recipe has more quantity of lemonade concentrate.
Therefore, Anna's recipe has stronger lemonade.
Problem 3 :
Look at the picture below.
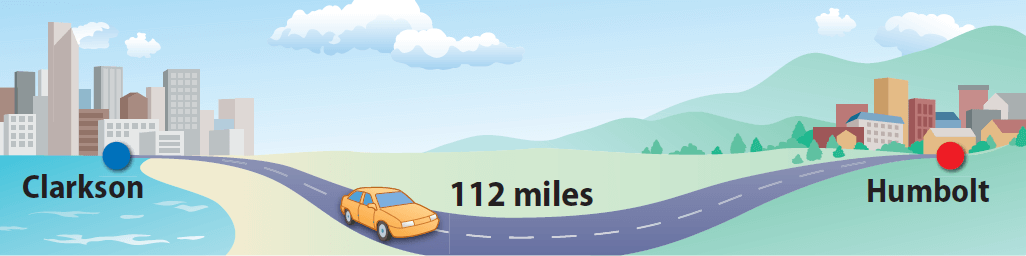
Janet drives from Clarkson to Humbolt in 2 hours. Suppose Janet drives for 10 hours. If she maintains the same driving rate, can she drive more than 600 miles? Justify your answer.
Solution :
A double number line is useful, because the regular intervals represent equivalent rates that compare different quantities. The one shown compares the number of miles driven to the time driven for different amounts of time.
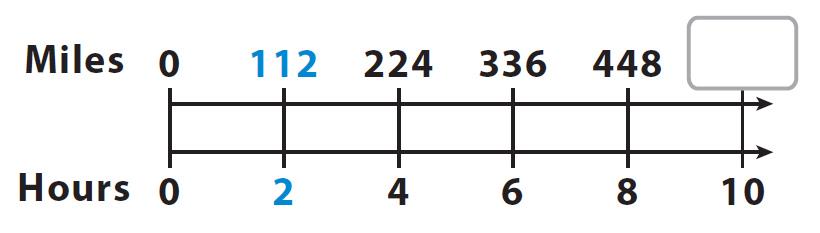
She covers 112 miles of distance in 2 hours. Since she maintains the same driving rate, every 2 hours, the distance covered will be increased by 112 miles.
In 8 hours she would have covered 448 miles of distance. After 2 hours, that is in 10 hours, the distance covered will be increased by 112 miles.
So, the distance covered in 10 hours is 560 miles.
It is shown in the picture given below.
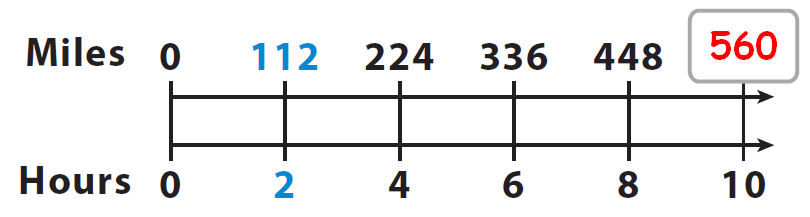
Conclusion :
From the above working, it is clear that she can not cover more than 600 miles in 10 hours, if she maintains the same driving rate.
Problem 4 :
In 15 minutes, Lena can finish 2 math problems. At that rate, how many math problems can she finish in 75 minutes ? Use a double number line to find the answer.
Solution :
The one shown compares the number of minutes to the number of math problems.
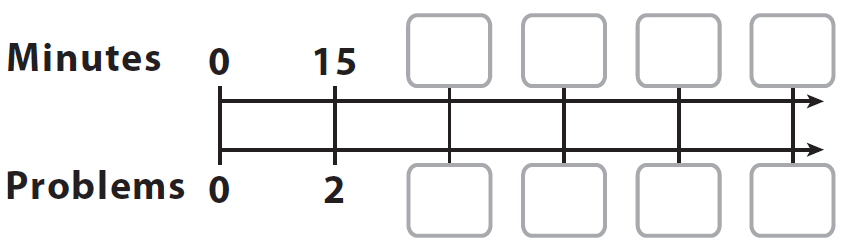
She finishes 2 math problems in 15 minutes. At this rate, every 15 minutes, the number of math problems finished will be increased by 2.
Let us mark this situation in the above double number line.
Than, we have
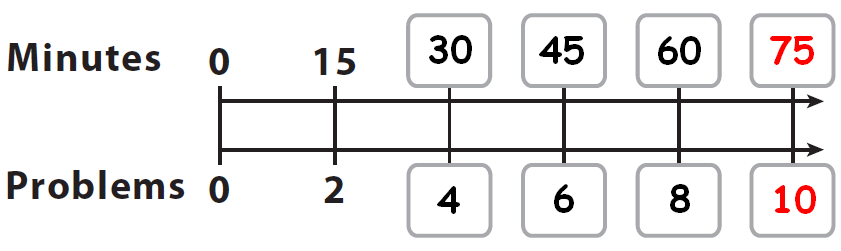
From the double number line, it is clear that she can finish 10 math problems in 75 minutes.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
