USING RATIONAL NUMBERS IN REAL LIFE

Fractions, integers, numbers with terminating decimal and numbers with repeating decimal are considered to be rational numbers.

All numbers are rational except of complex and irrational (π,root of imperfect numbers). So, rational numbers are used everywhere in real life leaving some special cases.

Example 1 : 

Malachi hikes for 2.5 miles and stops for lunch. Then he hikes for 1.5 more miles. How many miles did he hike altogether?

Solution : 

Step 1 : 

Use positive numbers to represent the distance Malachi hiked. 

Step 2 : 

Find 2.5 + 1.5.

Let us use the real number line to add 2.5 and 1.5.

Step 3 : 

Start at 2.5.

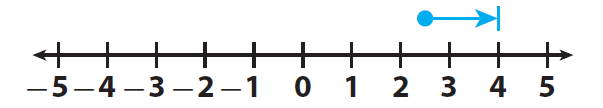
Step 4 : 

Move 1.5 units to the right because the second addend is positive.

The result is 4.

Malachi hiked 4 miles.

Example 2 : 

The temperature on an outdoor thermometer on Monday was 5.5 °C. The temperature on Thursday was 7.25 degrees less than the temperature on Monday. What was the temperature on Thursday ?

Answer : 

Step 1 : 

Find 5.5 - 7.25.

Step 2 :

Start at 5.5.

Step 3 :

Move |7.25| = 7.25 units to the left, because we are subtracting a positive numbe

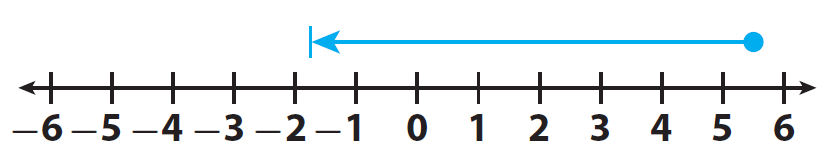
The result is -1.75.

The temperature on Thursday was -1.75 °C.

Example 3 : 

The science teacher is filling her new fish aquarium. The aquarium holds 40 gallons. If she fills the aquarium 4/5 of the way full, how many gallons will she need?

Solution :

If 4/5 of the aquarium is filled, then 1/5 th of the aquarium to be filled to make it full. Because 5 - 4  =  1.

To find number of gallons, we have to multiply 40 by 1/5. 

Step 1 : Multiply 40 by 1/5

40 x 1/5     

Step 2 : Simplify

8 x 1/1

Step 3 : Multiply 

8 x 1/1  =  8    

So, the science teacher needs 8 gallons to make the aquarium full. 

Example 4 : 

Maya wants to divide a 3/4 -pound box of trail mix into small bags. Each bag will hold 1/12 pound of trail mix. How many bags of trail mix can Maya fill ?

Solution : 

Step 1 : 

To get answer for the above question, we have to divide 3/4 by 1/12.

That is, we have to find the value of (3/4) / (1/12).

Step 2 : 

Determine the sign of the quotient.

The quotient will be positive, because the signs of both numerator (3/4) and denominator (1/12) are same. 

Step 3 : 

Write the complex fraction as division :

(3/4) / (1/12)  =  (3/4) ÷ (1/12)

Step 4 : 

Rewrite the above division as multiplication by taking the reciprocal of the second fraction. 

(3/4) ÷ (1/12)  =  (3/4) x (12/1)

Step 5 : 

Simplify

(3/4) x (12/1)  =  (3/1) x (3/1)

(3/4) x (12/1)  =  9

So, Maya can fill 9 bags of trail mix.

Example 5 :

Cooper's bird feeder holds 9/10 of a cup of birdseed. Cooper is filling the bird feeder with a scoop that holds 3/10 of a cup. How many scoops of birdseed will Cooper put into the feeder?

Solution : 

Step 1 : 

To get answer for the above question, divide the total amount of birdseed by the size of each scoop.

That is, we have to find the value of (9/10) / (3/10).

Step 2 : 

Determine the sign of the quotient.

The quotient will be positive, because the signs of both numerator (9/10) and denominator (3/10) are same. 

Step 3 : 

Write the complex fraction as division :

(9/10) / (3/10)  =  (9/10) ÷ (3/10)

Step 4 : 

Rewrite the above division as multiplication by taking the reciprocal of the second fraction. 

(9/10) ÷ (3/10)  =  (9/10) x (10/3)

Step 5 : 

Simplify

(9/10) x (10/3)  =  (3/1) x (1/1)

(9/10) x (10/3)  =  3

So, Cooper will put 3 scoops of birdseed into the feeder.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.