USING RATIO REASONING TO SOLVE PROBLEMS

Example 1 :

Sheldon and Leonard are partners in a business. Sheldon makes $2 in profits for every $5 that Leonard makes. If together they make a profit of $28 on the first item they sell, how much profit does Sheldon make ?

Solution :

Step 1 :

Given : Sheldon’s profit is $2 and Leonard's profit is $5.

Total profit = 2 + 5 = $7.

The ratio of Sheldon’s profit to the total profit is

$2/$7

Let S be the Sheldon's profit for the given total profit $28.

Then, we have

Step 2 :

Let us use ratio reasoning to find S.

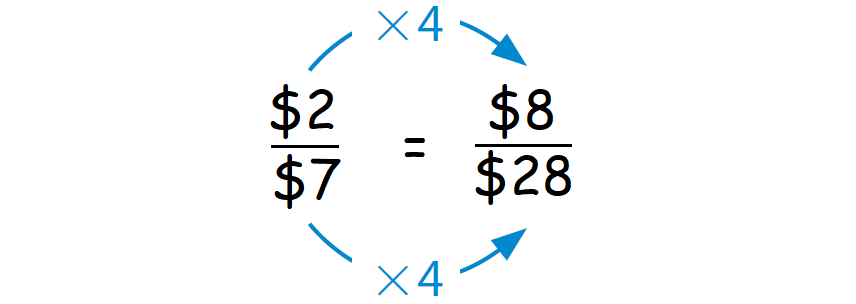
Because $7 x 4 = $28, multiply $2 by 4.

Therefore, if they make a total profit of $28, then Sheldon makes a profit of $8.

Example 2 :

The members of the PTA are ordering pizza for a meeting. They plan to order 2 cheese pizzas for every 3 pepperoni pizzas they order. How many cheese pizzas will they order if they order a total of 25 pizzas ?

Solution :

Step 1 :

Given : 2 cheese pizzas for every 3 pepperoni pizzas.

Total profit = 2 + 3 = 5 pizzas

The ratio of cheese pizzas to total pizzas is

2/5

Let C be the number of cheese pizzas for the given total pizzas 25.

Then, we have

Step 2 :

Let us use ratio reasoning to find C.

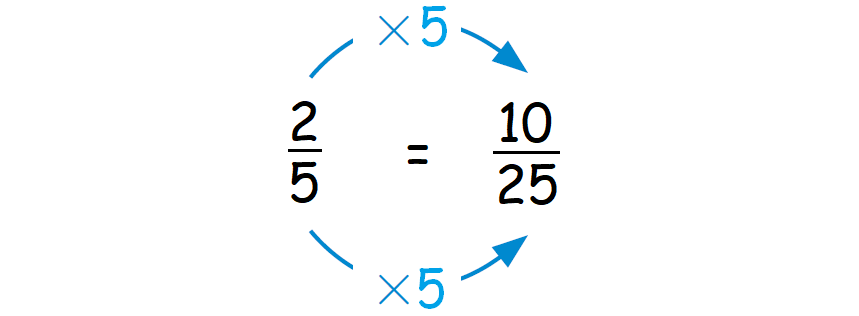
Because 5 × 5 = 25, multiply 2 by 5.

Therefore, if they order a total of 25 pizzas, then they will order 10 cheese pizzas.

Example 3 :

In a fruit bowl, there are 2 oranges for every 3 apples. If there are 15 apples, how many oranges are there?

Solution :

Ratio between oranges to apples = 2 : 3

When number of apples = 15, let x be the number of oranges.

2 : 3 = x : 15

2/3 = x/15

Since we have fractions on both sides, we have to do cross multiplication.

2(15) = 3x

x = 30/3

x = 10

Example 4 :

Rupra is picking strawberries. For every 5 strawberries she puts in her basket, she eats 2. If she picks 28 strawberries, how many does she eat and how many does she put in the basket?

Solution :

For every 5 strawberries she puts, she eats 2. From this, for every 7 stawberries she picks, she puts 5 in basket and she eats 2.

Ratio between number of strawberries she picks to number of strawberries she eats,

= 7 : 2

Let x be the number of strawberries she eats when she picks 28.

7 : 2 = 28 : x 

7/2 = 28/x

7x = 28(2)

x = 56/7

x = 8

Ratio between number of strawberries she picks to number of strawberries she puts,

= 7 : 5

Let y be the number of strawberries she puts when she picks 28.

7 : 5 = 28 : y

7/5 = 28/y

7y = 28(5)

y = 28(5) / 7

y = 4(5)

y = 20

Example 5 :

A bag of sweets contains red sweets and yellow sweets. The ratio of red to yellow is 3:7. If there are 40 sweets altogether, how many yellow sweets are there?

Solution :

Ratio between red to yellow sweets = 3 : 7

Let x be the number of yellow sweets.

Total number of sweets = 40

Then red sweets will be = 40 - x

(40 - x) : x = 3 : 7

(40 - x)/x = 3/7

7(40 - x) = 3x

280 - 7x = 3x

280 = 3x + 7x

280 = 10x

x = 280/10

x = 28

So, number of yellow sweets = 28

Number of red sweets = 40 - 28

= 12

Example 6 :

Jack has 30 sweets. He shares his sweets with his friend. When he gives his friend a sweet, he has 2 for himself. How many sweets do they each have?

Solution :

Ratio between number of sweets given to his friend and he has himself = 1 : 2

Number of sweets given to his friend = x

Number of sweets has himself = 2x

1x + 2x = 30

3x = 30

x = 30/3

x = 10

Number of sweets given to his friend = 10

Number of sweets has himself = 2(10) ==> 20

Example 7 :

In a field, there are some sheep and some goats. The ratio of sheep to goats is 3:1. If there are 3 goats, how many sheep are there?

Solution :

Ratio between sheeps to goats = 3 : 1

When number of goats = 3, then x be the number of sheeps.

x : 3 = 3 : 1

x/3 = 3/1

x = 9

So, the required number of sheeps is 9.

Example 8 :

Lucy has a necklace which has red beads and blue beads. For every red bead, there are four blue beads. There are 20 beads in total. How many of these are blue?

Solution :

Ratio between to red bead to blue bead = 1 : 4

Total number of beads = 20

Number of red bead = 1x

Number of blue bead = 4x

1x + 4x = 20

5x = 20

x = 20/5

x = 4

Number of red bead = 4

Number of blue bead = 4(4) ==> 16

So, number of blue bead is 16.

Example 9 :

Steffi is painting her house. She has calculated she needs 40 litres of paint in total. She has decided to mix pink paint. She will need 3 litres of white for every 2 litres of red. How many litres of each colour will she need to buy?

Solution :

Ratio between white colour to red colour = 3 : 2

Total quantity of paint = 40 liter

Quantity of white colour paint = 3x

Quantity of red colour paint = 2x

3x + 2x = 40

5x = 40

x = 40/5

x = 8

Quantity of white colour paint needs = 3(8) ==> 24 liter

Quantity of red colour paint needs = 2(8) ==> 16 liter

Example 10 :

In a pack of balloons, there are 3 different colours: red, blue and green. The ratio is 5:2:1 (red: blue: green). If there are 8 blue balloons in the pack, how many balloons are there in total?

Solution :

Ratio between red, blue and green balloons = 5 : 2 : 1

Total number of blue balloon = 2x

2x = 8

x = 8/2

x = 4

Number of red balloons = 5x ==> 5(4) ==> 20

Number of blue balloons = 2x ==> 2(4) ==> 8

Number of green balloons = 1x ==> 1(4) ==> 4

Total number of balloons = 20 + 8 + 4

= 32 balloons

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.