USING PYTHAGOREAN THEOREM TO FIND DISTANCE BETWEEN TWO POINTS

The Pythagorean Theorem

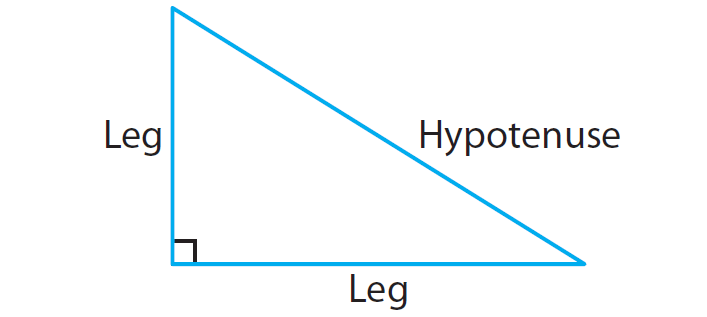
In a right triangle, the sum of the squares of the lengths of the  legs is equal to the square of the length of the hypotenuse.

If a and b are legs and c is the hypotenuse, then

a² + b²  =  c²

Using Pythagorean Theorem to Find Distance Between Two Points

Example 1 : 

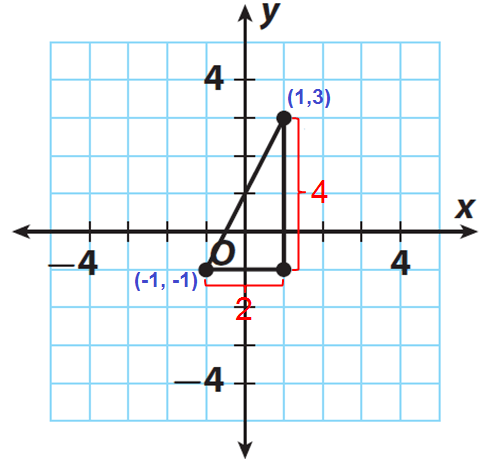
Find the distance between the points (1, 3) and (-1, -1) using Pythagorean theorem. Check your answer for reasonableness.

Solution : 

Step 1 :

Locate the points (1, 3) and (-1, -1) on a coordinate plane.

Step 2 :

Draw horizontal segment of length 2 units from (-1, -1)  and vertical segment of length of 4 units from (1, 3) as shown in the figure. 

Step 3 :

Find the length of each leg.

The length of the vertical leg is 4 units.

The length of the horizontal leg is 2 units. 

Step 4 :

Let a = 4 and b = 2 and c represent the length of the hypotenuse.

Because a and b are legs and c is hypotenuse, by Pythagorean Theorem, we have

a² + b²  =  c²

Step 5 :

Plug a  = 4 and b = 2 in (a² + b²  =  c²⁾ to solve for c. 

4² + 2²  =  c²

Simplify.

16 + 4  =  c²

20  =  c²

Take the square root of both sides.

√20  =  √c²

√20  =  c

Step 6 :

Find the value of √20 using calculator and round to the nearest tenth

4.5  ≈  c

Step 7 :

Check for reasonableness by finding perfect squares close to 20.

√20 is between √16 and √25, so 4 < √20 < 5.

Since 4.5 is between 4 and 5, the answer is reasonable.

Hence, the distance between the points (1, 3) and (-1, -1) is about 4.5 units. 

Example 2 : 

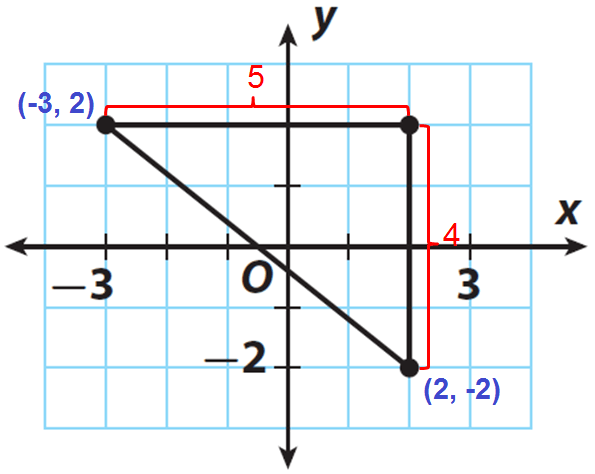
Find the distance between the points (-3, 2) and (2, -2) using Pythagorean theorem. Check your answer for reasonableness.

Solution : 

Step 1 :

Locate the points (-3, 2) and (2, -2) on a coordinate plane.

Step 2 :

Draw horizontal segment of length 5 units from (-3, -2)  and vertical segment of length of 4 units from (2, -2) as shown in the figure. 

Step 3 :

Find the length of each leg.

The length of the vertical leg is 4 units.

The length of the horizontal leg is 5 units. 

Step 4 :

Let a = 4 and b = 5 and c represent the length of the hypotenuse.

Because a and b are legs and c is hypotenuse, by Pythagorean Theorem, we have

a² + b²  =  c²

Step 5 :

Substitute a = 4 and b = 5 in (a² + b²  =  c²) to solve for c. 

4² + 5²  =  c²

Simplify.

16 + 25  =  c²

41  =  c²

Take the square root of both sides.

√41  =  √c²

√41  =  c

Step 6 :

Find the value of √41 using calculator and round to the nearest tenth

6.4  ≈  c

Step 7 :

Check for reasonableness by finding perfect squares close to 41.

√41 is between √36 and √49, so 6 < √41 < 7.

Since 6.4 is between 6 and 7, the answer is reasonable.

Hence, the distance between the points (-3, 2) and (2, -2)  is about 4.5 units. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.