USING PROPERTIES OF PARALLEL LINES

In this section, we are going to see how the properties of parallel lines can be used to verify whether two lines are parallel.

Just remember that when it comes to proving two lines are parallel, all we have to look at are the angles. Specifically, we want to look for pairs of :

(i) Corresponding angles

(ii) Alternate interior angles

(iii) Alternate exterior angles, or

(iv) Supplementary angles

Corresponding Angles Converse

If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

The diagram given below illustrates this.

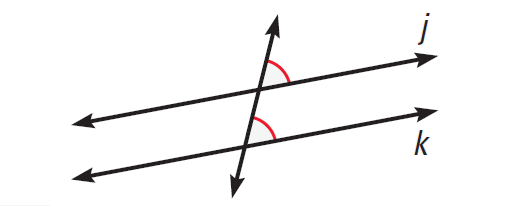
In the diagram above, j||k.

Alternate Interior Angles Converse

If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel.

The diagram given below illustrates this.

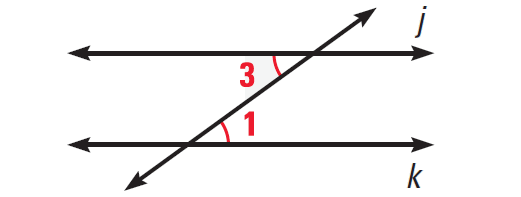
In the diagram above, if ∠1 ≅ ∠3, then j||k.

Consecutive Interior Angles Converse

If two lines are cut by a transversal so that consecutive interior angles are supplementary, then the lines are parallel.

The diagram given below illustrates this.

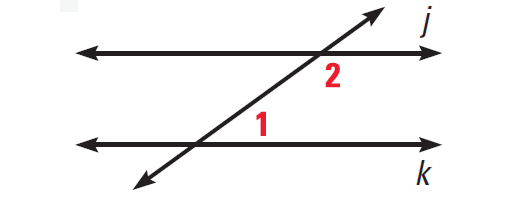
In the diagram above, if ∠1 + ∠2 = 180°, then j||k.

Alternate Interior Angles Converse

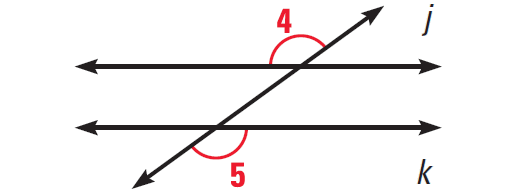
In the diagram above, if ∠4 ≅ ∠5, then j||k.

Transitive Property of Parallel Lines

If two lines are parallel to the same line, then they are parallel to each other.

The diagram given below illustrates this.

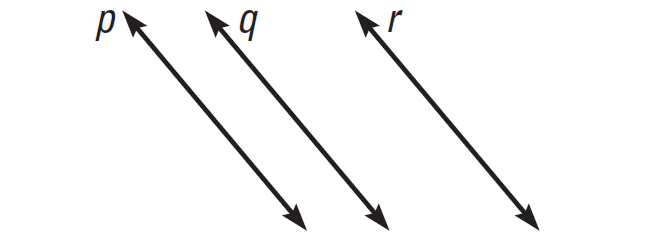
In the figure above, if p||q and q||r, then p||r.

Lines Perpendicular to a Transversal Theorem

In a plane, if two lines are perpendicular to the same line, then they are parallel to each other.

The diagram given below illustrates this.

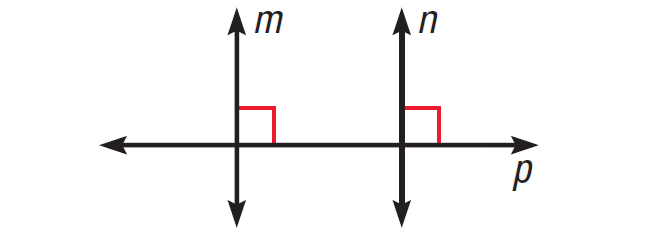
In the figure above, if m ⊥ p and n ⊥ p, then m||n.

Solving Problems Using Properties of Parallel Lines

Problem 1 :

In the diagram given below, lines m, n and k represent three of the oars. If m||n and n||k, then prove m||k.

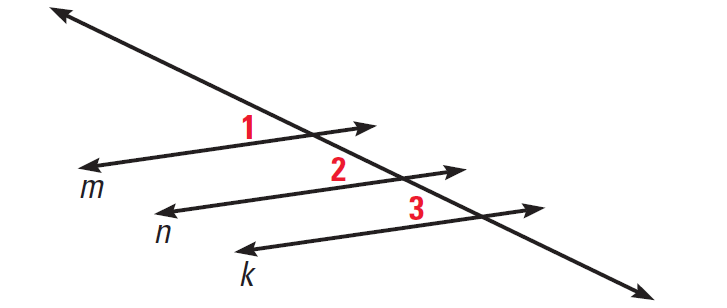
Solution :

Problem 2 :

In the diagram given below, if ∠1 ≅ ∠2, then prove m||n.

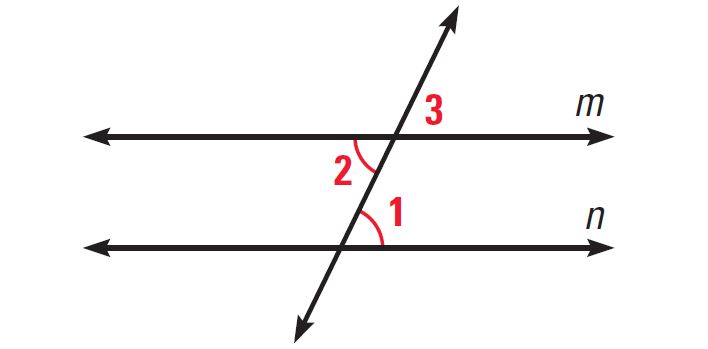
Solution :

Problem 3 :

In the diagram given below, each line is parallel to the next immediate line. Explain why the line K₁ is parallel to the line K₂.

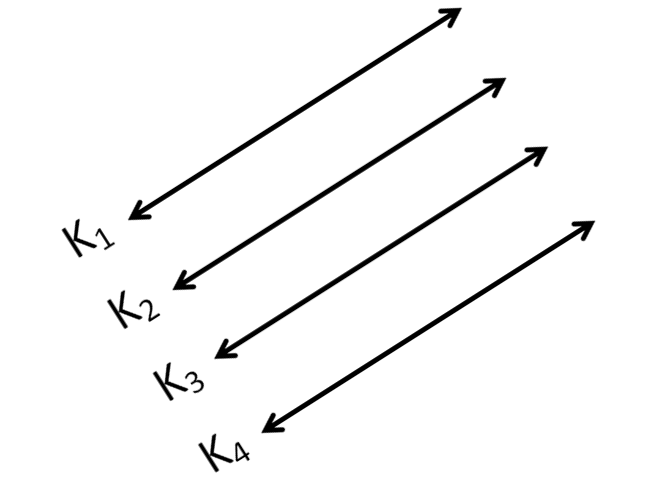
Solution :

We are given that K₁||K₂ and K₂||K_3.

By transitive property of parallel lines, K₁||K_3.

Since K₁||K₃ and K₃||K₄, again by transitive property, it follows that K₁||K_4.

Problem 4 :

In the diagram given below, lines a and b are perpendicular to the line c. Prove that the lines a and b are parallel.

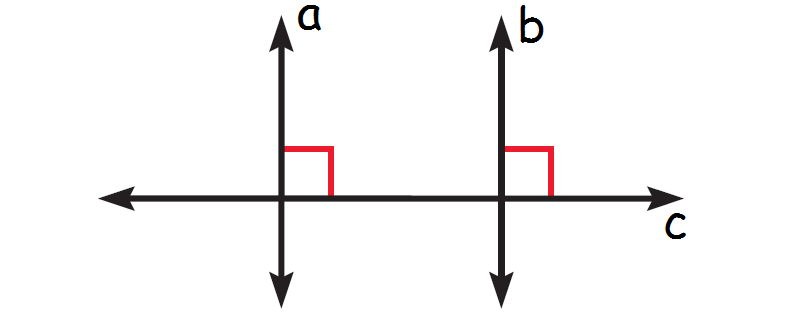
Solution :

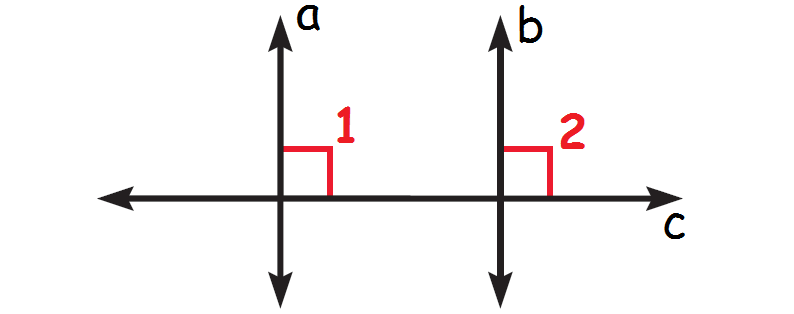
Since the line c cuts both the lines a and b, the line c is transversal. Both the lines a and b are perpendicular to the line c. So,  the measure of both ∠1 and ∠2 in the above diagram is 90° and c is transversal to the lines a and b.

That is,

m∠1 = 90°

m∠2 = 90°

By corresponding angles converse, the lines a and b are parallel.

Problem 5 :

In the diagram given below, if ∠4 and ∠5 are supplementary, then prove g||h.

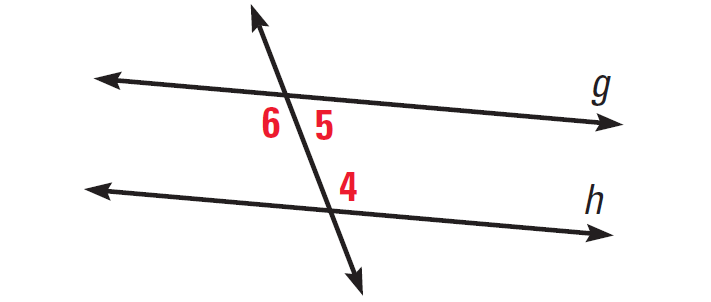
Solution :

We are given that ∠4 and ∠5 are supplementary. By the linear pair postulate, ∠5 and ∠6 are also supplementary, because they form a linear pair. By the congruence supplements theorem, it follows that ∠4 ≅ ∠6. Therefore, by the alternate interior angles converse, g and h are parallel.

Problem 6 :

In the diagram given below, find the value of x that makes j||k.

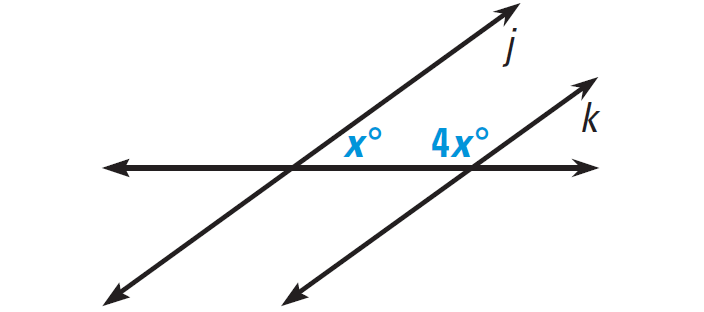
Solution :

Lines j and k will be parallel if the marked angles are supplementary.

x° + 4x° = 180°

5x = 180

x = 36

So, x = 36 makes j||k.

Problem 7 : 

If two boats sail at a 45° angle to the wind as shown, and the wind is constant, will their paths ever cross ? Explain.

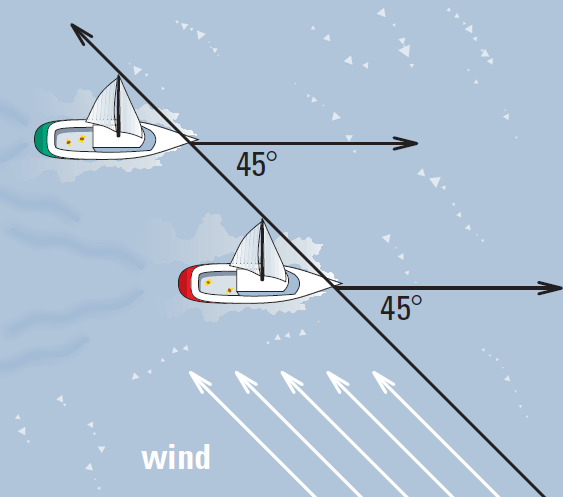
Solution :

Because corresponding angles are congruent, the paths of the boats are parallel. Parallel lines do not intersect. So the paths of the boats will never cross.

Problem 8 :

In the diagram given below, decide which rays are parallel.

(i) Is EB parallel to HD?

(ii) Is EA parallel to HC?

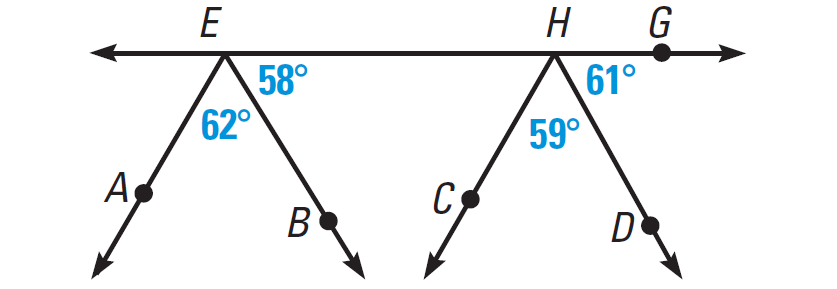
Solution (i) :

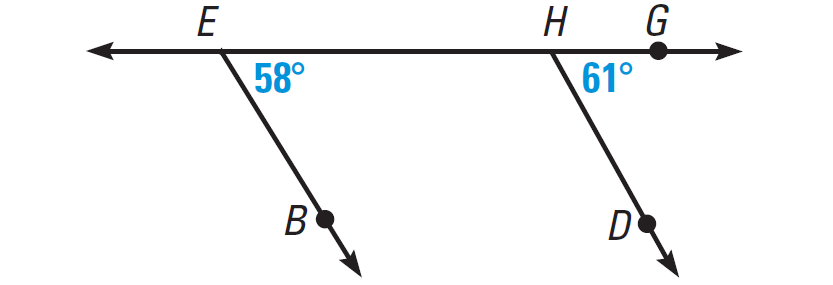
m∠BEH  =  58°

m∠DHG  =  61°

∠BEH and ∠DHG are corresponding angles, but they are not congruent. So EB and HD are not parallel.

Solution (ii) :

m∠AEH = 62° + 58° = 120°

m∠CHG = 59° + 61° = 120°

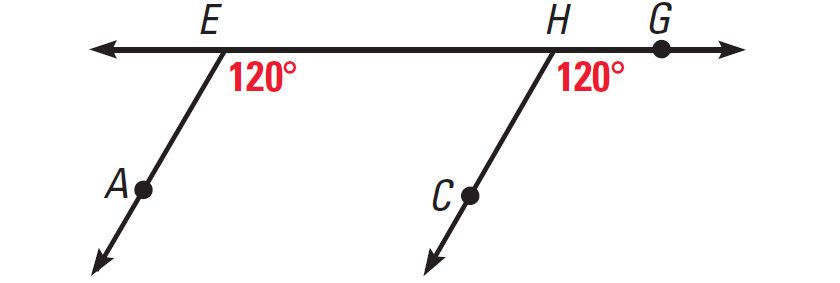
∠AEH and ∠CHG are congruent corresponding angles. So AE and CH are parallel.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.