USING DIVISION TO SOLVE EQUATIONS

Example 1 :

Solve the following equation and graph the solution on a number line.

9a = 54

Solution :

9a = 54

Since we are trying to solve for 'a', we have to get rid of '9' which is multiplied by a in the above equation.

To get rid of 9, we have to divide both sides of the equation by 9.

9a/9 = 54/9

a = 6

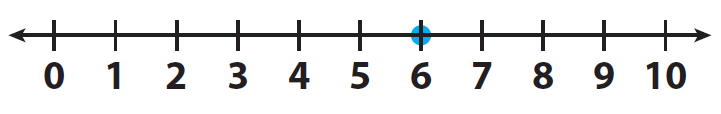
Example 2 :

Solve the following equation and and graph the solution on a number line.

Solution :

18 = 6d

Divide both sides by 6.

18/6 = 6d/6

3 = d

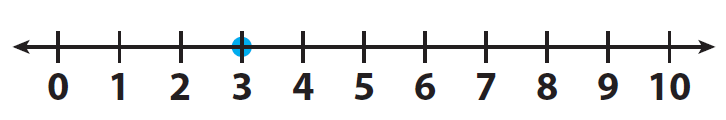
Example 3 :

The product of two numbers is 20. If one number is 8, find the other number.

Solution :

Let x be the other number.

8x = 20

Divide both sides by 8.

8x/8 = 20/8

x = 2.5

The other number is 2.5.

Example 4 :

Three times of x is equal to four times of y. If the value of y is 6, find the value of x.

Solution :

Given : Three times of x is equal to four times of y.

3x = 4y

Substitute y = 6.

3x = 4(6)

3x = 24

Divide each both sides by 3.

3x/3 = 24/3

x = 8

Example 5 :

Deanna has a recipe for potato cakes that requires 12 eggs to make 3 batches of potato cakes. Represent the given situation as an equation.

Model the equation and find how many eggs are needed per batch.

Solution :

Write a word equation based on the situation.

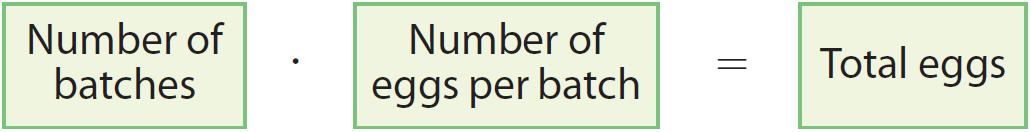
Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.

Let x represent the number of eggs needed per batch.

Then, we have

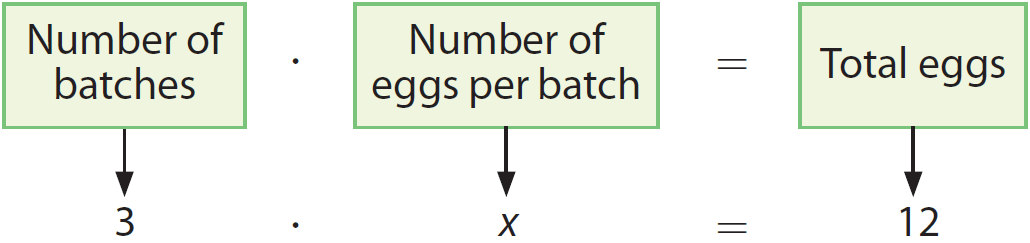
Therefore, the equation 3x = 12 represents the given situation.

Let us model the equation 3x = 12 using algebra tiles.

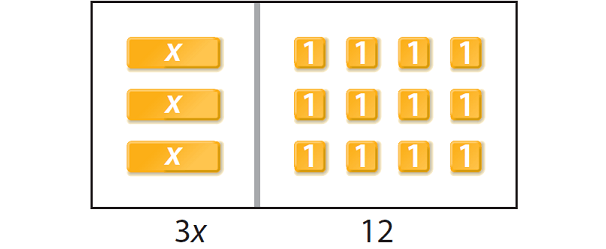
To find how many eggs are needed per batch, we have to solve for x.

To solve for x in the above model, we have to isolate x.

There are three x tiles, so draw circles to separate the tiles into 3 equal groups.

One group has been circled here.

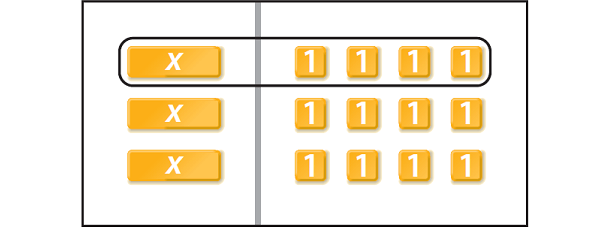
In the circled group above, we find one x on the left side and four 1 tiles on the right side.

So, the value of x is 4.

Hence, 4 eggs are needed per batch.

Example 6 :

A discounted amusement park ticket costs $12.95 less than the original price p. Write and solve an equation to find the original price.

Solution :

p be the original price

Discounted price = p - 12.95

Discounted price from the poster = 44

p - 12.95 = 44

p = 44 + 12.95

 = 56.95

So, the origial price is $56.95 

Example 7 :

A baker orders 162 eggs. Each carton contains 18 eggs. Which equation can you use to find the number x of cartons? Explain your reasoning and solve the equation.

a)  162x = 18    b)  x — 18 = 162

c) 18x = 162      d)  x + 18 = 162

Solution :

Number of eggs in each carton = 18

Number of eggs ordered = 162 eggs

x be the number of cartons.

18x = 162

So, option c is correct.

Example 8 :

The length of an American flag is 1.9 times its width. What is the width of the flag

Solution :

Length of flag = 9.5 ft

Let w be the width of the flag.

Lenght of flag = 1.9w

1.9w = 9.5

w = 9.5/1.9

w = 5

So, the width of the flag is 5 ft.

Example 9 :

The balance of an investment account is $308 more than the balance 4 years ago. The current balance of the account is $4708. What was the balance 4 years ago?

Solution :

Let x be the balance amount 4 years ago.

The current balance = $4708

x + 308 = 4708

x = 4708 - 308

x = 4400

So, the balance 4 years ago is $4400.

Example 10 :

Tatami mats are used as a floor covering in Japan. One possible layout uses four identical rectangular mats and one square mat, as shown. The area of the square mat is half the area of one of the rectangular mats.

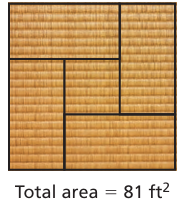
a. Write and solve an equation to find the area of one rectangular mat.

b. The length of a rectangular mat is twice the width. Find the dimensions of one rectangular mat.

Solution :

a) Let w be the width of the rectangular field.

length = 2w

a) Area of 4 rectangular field + area of square field

= 81 ft²

b)

4[2w (w)] + w (w) = 81

8w² + w² = 81

9w² = 81

w² = 81/9

w² = 9

w = 3 ft

Length = 2(3) ==> 6 ft

So, length and width of rectangular field is 6 ft and 3 ft.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.