USING CONVERSION FACTORS WORKSHEET

Detailed Answer Key

1. Answer :

Step 1 :

We want to convert gallons to quarts.

Identify the ratio that compares the units involved.

The units gallons and quarts are customary units of capacity.

Find the relationship of those units in the capacity section of the customary measurements table.

4 quarts  =  1 gallon

The appropriate conversion factor is 4/1.

Because when we multiply 2 gallons by that conversion factor, we can divide out the common unit gallons. The resulting unit is quarts.

Step 2 :

Multiply the given measurement by the conversion factor.

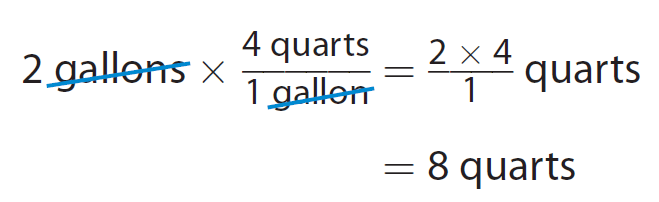
Elena needs 8 quarts of milk.

2. Answer :

Step 1 :

You want to convert kilograms to milligrams.

There is no equation in the table that relates kilograms and milligrams directly. However, we can convert kilograms to grams first. Then we can convert grams to milligrams.

Step 2 :

Multiply the given measurement by the conversion factor.

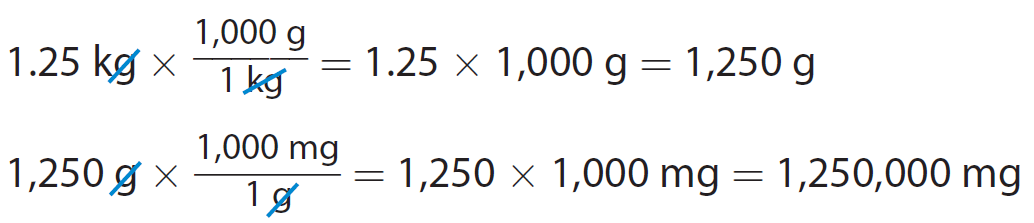
We can also do both conversions at the same time.

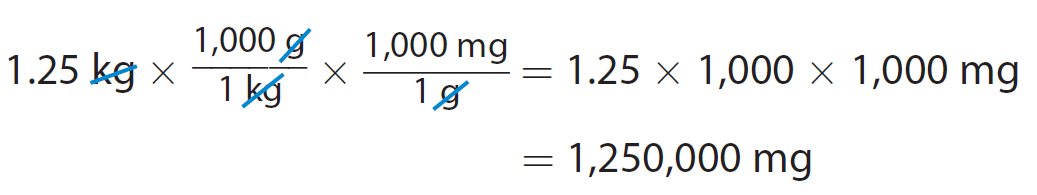
A mass of 1.25 kilograms is equal to 1,250,000 milligrams.

3. Answer :

Step 1 :

Find the conversion factor for converting kilograms to pounds

1 kilogram ≃  2.20 pounds

Write the conversion factor as a ratio

2.20 pounds / 1 kilogram

Step 2 :

Convert the given measurement.

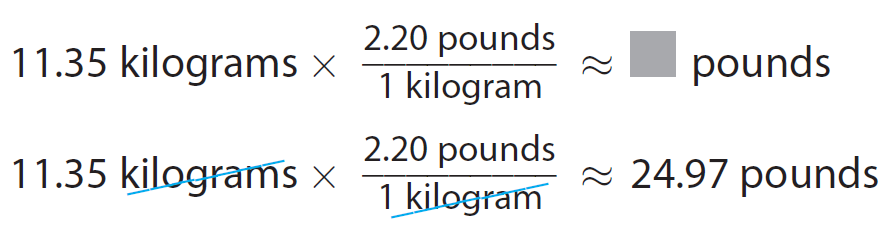
Alima adds about 25 pounds.

4. Answer :

Step 1 :

First find the dimensions of the driveway in meters.

Convert each measurement to meters.

Use 1 foot ≃ 0.305 meter.

Step 2 :

Next find the area in square meters.

Area  =  length × width

≃  13.725 × 5.49

≃  75.35025 square meters

Step 3 :

Now find the total cost of the paving.

square meters × cost per square meter = total cost

75.35025 × $24 ≃ $1,808.41

Total cost of the paving is $1808.41.

5. Answer :

Step 1 :

We want to convert gallons to quarts.

Identify the ratio that compares the units involved.

The units centimeters and meters are metric units length.

Find the relationship of those units in the length section of the metric measurements table.

1 meter  =  100 centimeters

The appropriate conversion factor is 1/100.

Because when we multiply 250 centimeters by the conversion factor, we can divide out the common unit centimeters. The resulting unit is meters.

Step 2 :

Multiply the given measurement by the conversion factor.

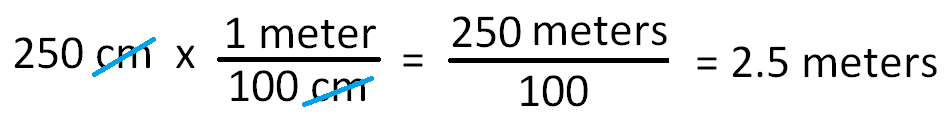
Height of the oak tree is 2.5 meters. 

6. Answer :

Each aspirin can take = 500 milligrams

Number of aspirins = 4

Weight of all 4 packs = 4(500)

= 2000 milligrams

Converting milligrams to kilograms, we get

1000 milligrams = 1 kilogram

2000 milligrams = 2 kilograms

So, weight of all 4 packs is 2 kilograms.

7. Answer :

Quantity of water that wildcats’ water cooler holds = 15 liter

1 liter = 1000 milliliter

Multiplying both sides by 15, we get

15 liters = 15(1000) 

= 15000 milliliters

8. Answer :

The distance covered by snail per second = 0.013 meters

1 meter = 100 centimeter

To convert meter to centimeter, we have to multiply by 1000.

= 0.013 x 1000

= 13 centimeters

So, snail is moving 13 centimeters per seconds.

9. Answer :

Length of ribbon = 8 yards

Measure of each ribbon to cut off = 1  1/2 yards

= 3/2 yards

Number of pieces = 8/(3/2)

= 8 x (2/3)

= 16/3

= 5.3

approximately 5 pieces.

10. Answer :

Minimum weight of Ishi = 70 kilograms

1 kilogram = 1000 grams

= 70 x 1000

= 70000 grams

11. Answer :

Time taken to reach dance studio = 48 minutes

Time taken to reach home = 1 hour 7 minutes

Total time taken = 48 minutes + 1 hour 7 minutes

= 1 hour + (48 + 7) minutes

= 1 hour 55 minutes

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.