USING CONGRUENT TRIANGLES

Knowing that all pairs of corresponding parts of congruent triangles are congruent can help us to reach conclusions about congruent figures.

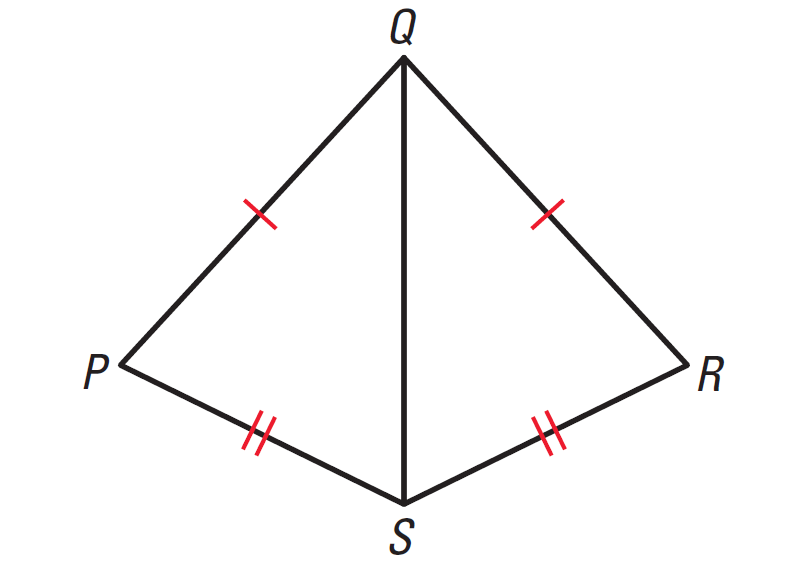
For instance, suppose we want to prove that

∠PQS ≅ ∠RQS

in the diagram shown below. One way to do this is to show that ΔPQS ≅ ΔRQS by the SSS congruence postulate. Then we can use the fact that corresponding parts of congruent triangles are congruent to conclude that

∠PQS ≅ ∠RQS

Example 1 : 

In the diagram shown below, AB || CD, BC || DA. Prove that

AB ≅ CD

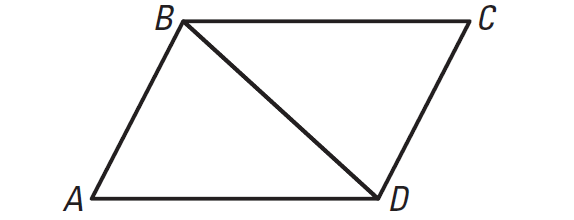
Plane for Proof :

Show that ΔABD ≅ ΔCDB. Then use the fact that corresponding parts of congruent triangles are congruent.

Solution :

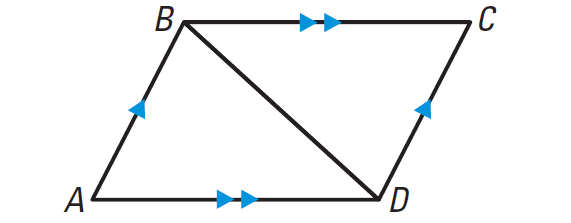
First copy the diagram and mark it with the given information. Then mark any additional information that we can deduce. Because AB and CD are parallel segments intersected by a transversal, BC and DA are parallel segments intersected by a transversal, we can deduce that two pairs of alternate interior angles are congruent.

Mark Given Information :

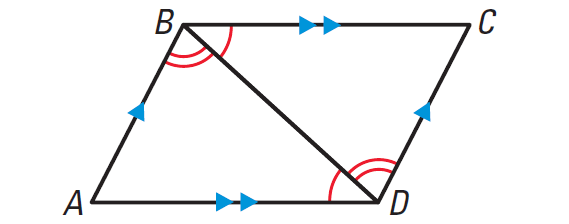
Add Deduced Information :

Paragraph Proof :

Because AB || CD, it follows from the Alternate Interior Angles Theorem, that ∠ABD ≅ ∠CDB. For the same reason, ∠ADB ≅ ∠CBD, because BC || DA. By the Reflexive Property of Congruence, BD ≅ BD. We can use the ASA congruence postulate to conclude that

ΔABD ≅ ΔCDB

Finally, because corresponding parts of congruent triangles are congruent, it follows that

AB ≅ CD

Example 2 :

In the diagram shown below,

A is the midpoint of MT

A is the midpoint of SR

Prove that MS || TR.

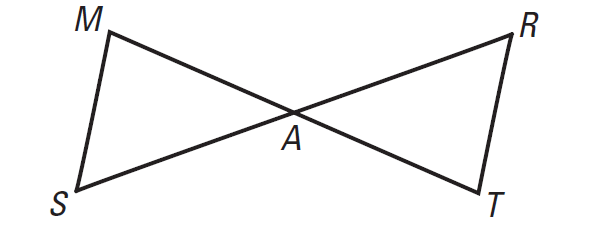
Plane for Proof :

Prove that ΔMAS ≅ ΔTAR. Then use the fact that corresponding parts of congruent triangles are congruent to show that ∠M ≅ ∠T. Because these angles are formed by two segments intersected by a transversal, we can conclude that MS || TR.

Solution :

Example 3 :

In the diagram shown below,

∠1 ≅ ∠2

∠3 ≅ ∠4

Prove that ΔBCE ≅ ΔDCE.

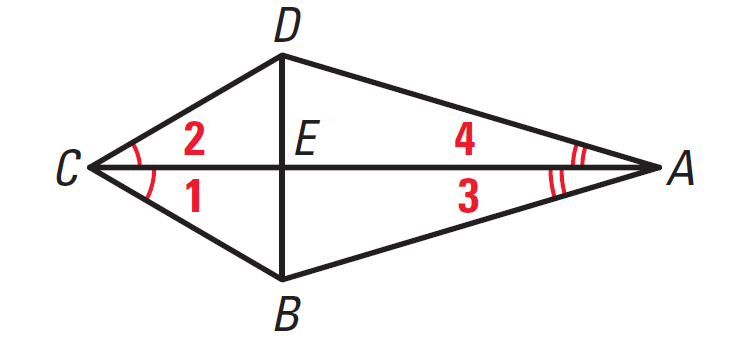
Plane for Proof :

The only information we have about ΔBCE and ΔDCE is that ∠1 ≅ ∠2 and that CE ≅ CE. Notice, however, that sides BC and DC are also sides of ΔABC and ΔADC. If we can prove that ΔABC ≅ ΔADC, we can use the fact that corresponding parts of congruent triangles are congruent to get a third piece of information about ΔBCE and ΔDCE.

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.