USE ORDER OF OPERATIONS TO EVALUATE EXPRESSIONS

The order of operations is a rule that tells the correct  sequence of steps for evaluating a math expression.

We can remember the order using PEMDAS :

Important Notes :

1. In a particular simplification, if you have both multiplication and division, do the operations one by one in the order from left to right.

2. Multiplication does not always come before division. We have to do one by one in the order from left to right.

3. In a particular simplification, if you have both addition and subtraction, do the operations one by one in the order from left to right.

Examples :

16 ÷ 4 x 3 = 4 x 3 = 12

18 - 3 + 6 = 15 + 6 = 21

In the above simplification, we have both division and multiplication. From left to right, we have division first and multiplication next.

So we do division first and multiplication next.

Evaluate each of the following numerical expressions.

Problem 1 :

[13 + 2(4)]/[3(5 - 4)]

Solution :

= [13 + 2(4)]/[3(5 - 4)]

= [13 + 8]/[3(1)]

= 21/ 3

= 7

Problem 2 :

(15 ⋅ 6)/(16 - 7)

Solution :

= (15 ⋅ 6)/(16 - 7)

= 90/9

= 10

Problem 3 :

[7(3) + 3]/[4(3 -1)] + 6

Solution :

= [7(3) + 3]/[4(3 -1)] + 6

= [21 + 3]/[4(2)] + 6

= 24/8 + 6

= 3 + 6

= 9

Problem 4 :

(1/4)[7(2³) + 4(5²) - 6(2)]

Solution :

= (1/4)[7(2³) + 4(5²) - 6(2)]

= (1/4)[7(8) + 4(25) - 6(2)]

= (1/4)[56 + 100 - 12]

= (1/4)[156 - 12]

= (1/4)[144]

= 36

Problem 5 :

[4(14 - 1)]/[3(6) - 5] + 7

Solution :

= [4(14 - 1)]/[3(6) - 5] + 7

= [4(13)]/[18 - 5] + 7

= 52/13 + 7

= 4 + 7

= 11

Problem 6 :

(1/8)[6(3²) + 2(4³) - 2(7)]

Solution :

= (1/8)[6(3²) + 2(4³) - 2(7)]

= (1/8)[6(9) + 2(64) - 14]

= (1/8)[54 + 128 - 14]

= (1/8)[182 - 14]

= (1/8)[168]

= 21

Problem 7 :

Before a show, there are 8 people in a theater. Five groups of 4 people enter, and then three groups of 2 people leave.

Evaluate the expression

8 + 5(4) − 3(2)

to find how many people are in the theater.

Solution :

= 8 + 5(4) − 3(2)

Using order of operation, we have to perform multiplicaiton first.

= 8 + 20 - 6

= 28 - 6

= 22

Problem 7 :

Th e front door of a house is painted white and blue. Each window is a square with a side length of 7 inches. What is the area of the door that is painted blue?

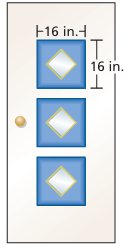
Solution :

Considering one square inside, the side length of square

= 16 inches

Side length of window = 7 inches

Area of one window to be painted with blue colour = 

16² - 7²

Three windows with same size, then the required area to be painted with blue colour.

= 3[16² - 7²]

= 3[256-49]

= 3(207)

= 621

So, the required area to be painted with the colour of blue is 621 square inches.

Problem 8 :

You buy 6 notebooks, 10 folders, 1 pack of pencils, and 1 lunch box for school. After using a $10 gift card, how much do you owe? Explain how you solved the problem.

Solution :

Cost of each notebook = $2

Cost of pack of pencil = $3

Cost of lunch box = $8

Cost of folder = $1

Amount spent = 6(2) + 10(1) + 1(3) + 1(8)

Gift worth of $10

Amount to owe = [6(2) + 10(1) + 1(3) + 1(8)] - 10

= [12 + 10 + 3 + 8] - 10

= 33 - 10

= 23

So, the amount to owe is $23.

Problem 9 :

A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis. How many cells are there after 14 days? Justify your answer.

Solution :

Number of cells in day 1 = 35

Since each cell is divided in to 2 cells in process, number of cells in day 2

= 35 (2)

= 70

Number of cells in day 3 = 70(2) 

= 140

can be expressed as = 2²(35)

Number of cells in day 4 = 140(2) 

= 280

can be expressed as = 2³(35)

Continuing the pattern,

number of cells in day 15 = number of cells after 14 days 

= 2¹⁴ (35)

Problem 10 :

Two groups collect litter along the side of a road. It takes each group 5 minutes to clean up a 200-yard section. How long does it take both groups working together to clean up 2 miles? Explain how you solved the problem.

Solution :

1 mile = 1760 yards

2 miles = 2(1760)

= 3520 yards

Time taken by one group to cover 200 yard sections 

= 5 minutes

Two groups working together within the same 5 minutes, they will cover 400 yard sections.

5 minutes = 400 yards

1 minute = 400/5

= 80 yards

Time = distance / speed

= 3520 / 80

= 44 minutes

So, the required time is 44 minutes.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.