UNIT RATE DEFINITION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Unit rate compares the given amount to one unit of another measure.
(or)
The ratio between the given value and 1.
(or)
Comparing the given amount or value to 1.
Examples :
1. If 8 dolls are made in 4 days, then number of dolls made in 1 day = 2.
2. If David earns $180 in 9 hours, then number of dollars earned by him in 1 hour = $20.
3. If there are 16 cups in 4 quarts, then the number of cups in 1 quart = 4.
Liquid Measurements - Unit Rates
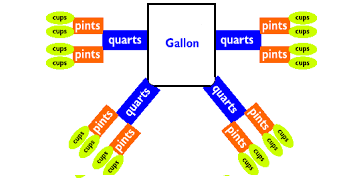
From the above picture, we can get the following unit rates related to liquid measurements.
1 gallon = 16 cups
1 gallon = 8 pints
1 gallon = 4 quarts
1 quart = 2 pints
1 quart = 4 cups
1 pint = 2 cups
Solved Problems
Problem 1 :
In a business, if A can earn $ 7500 in 2.5 years, find the unit rate of his earning per month.
Solution :
Given : Earning in 2.5 years = $7500.
1 year = 12 months
2.5 years = 2.5 x 12 = 30 months
Then, earning in 30 months = $7500.
Therefore, earning in 1 month = 7500/30 = $250.
Hence, the unit rate of his earning per month is $250.
Problem 2 :
If David can prepare 2 gallons of juice in 4 days, how many cups of juice can he prepare per day ?
Solution :
No. of gallons of juice prepared in 4 days = 2 gallons.
1 gallon = 16 cups
So, no. of cups of juice prepared in 4 days :
= 2 ⋅ 16
= 32 cups
Therefore, David can prepare 32 cups of juice in 4 days.
Then, no. of cups of juice prepared in 1 day :
= 32/4
= 8
Hence, David can prepare 8 cups of juice in 1 day.
Problem 3 :
If John can cover 360 miles in 3 hours, find the number of miles covered by John in 1 minute.
Solution :
No of miles covered in 3 hours = 360.
Then, no. of miles covered in 1 hour :
= 360/3
= 180
1 hour = 60 minutes
So, no. of miles covered in 60 minutes = 180.
Then, no. of miles covered 1 minute = 180/60 = 3.
Hence, John can cover 3 miles in 1 minute.
Problem 4 :
75 basketballs cost $1,143.75. Find the unit rate in price per basketball.
Solution :
Given :75 basketballs cost $1,143.75
Then, price pf one basket ball = 1143.75/75 = 15.25.
Hence, the unit rate in price per basket ball is $15.25.
Problem 5 :
In 36.5 weeks, Miguel raised $2,372.50 for cancer research. How was his unit rate in price per week?
Solution :
Given : Miguel raised $2, 372.50 in 36.5 weeks.
Then, amount raised in one week = 2372.5/36.5 = 65.
Hence, the unit rate in price per week was $65.
Problem 6 :
Shanel walks 2/5 of a mile every 1/7 hour. Express her speed as a unit rate in miles per hour.
Solution :
Given :Shanel walks 2/5 of a mile every 1/7 hour
We know the formula for speed.
Speed = Distance/Time
= (2/5)/(1/7)
= (2/5) ⋅ (7/1)
= 14/5
= 2.8 miles per hour
Hence, the speed of Shanel is 2.8 miles per hour.
Problem 7 :
Declan use 2/35 of a gallon of gas for every 4/5 of a mile that he drives. At this rate, how many miles can he drive on one gallon of gas?
Solution :
Given : In 2/35 of a gallon of gas, 4/5 of a mile is traveled
2/35 of a gallon of gas -----> 4/5 of a mile
1 gallon of gas -----> (4/5) ⋅ (35/2) miles
1 gallon of gas -----> 14 miles
Hence, Declan can drive 14 miles in 1 gallon of gas.
Problem 8 :
A person can cover a distance of 84 miles in 4 gallons of fuel. If he has 2.5 gallons, how many miles can he cover?
Solution :
Given : 84 miles can be traveled in 4 gallons.
Then, no. of miles traveled in 1 gallon = 84/4 = 21.
Therefore, no. of miles traveled in 2.5 gallons is
= 21 ⋅ 2.5
= 52.5
Hence, 52.5 miles traveled in 2.5 gallons of fuel.
Problem 9 :
If a person drinks 8 cups of apple juice per month, how many gallons will he drink in one year?
Solution :
Given :8 cups in one month
1 year = 12 months
So, no. of cups in 1 year = 8 ⋅ 12 = 96 cups.
1 gallon = 16 cups
Therefore, no. of gallons in 1 year :
= 96/16
= 6
Hence, he will drink 6 gallons of apple juice in 1 year.
Problem 10 :
My David earns $416 in 8 hours. How much does earn in 2.8 hours?
Solution :
Given : Earning in 8 hours = $416.
Earning in 1 hour = $ 52
Earning in 2.8 hours :
= 52 ⋅ 2.8
= 145.6
Hence, Mr. David will earn $145.6 in 2.8 hours.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

