THE UNIT CIRCLE

The set of points at a distance 1 from the origin is a circle of radius 1. 

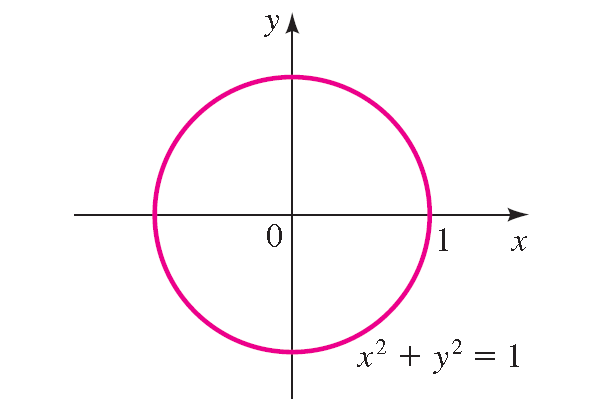
The unit circle is the circle of radius 1 centered at the origin in the xy-plane.

Its equation is

x² + y²  =  1

A Point on the Unit Circle

Example 1 :

Show that the point A(4/5, -3/5) is on the unit circle. 

Solution : 

We have to show that this point satisfies the equation of the unit circle, that is, x² + y² = 1. 

(4/5)² + (-3/5)²  =  16/25 + 9/25

=  (16 + 9)/25

=  25/25

=  1

So, A is on the unit circle. 

Example 2 :

Show that the point B(√3/3, √6/3) is on the unit circle. 

Solution : 

We have to show that this point satisfies the equation of the unit circle, that is, x² + y² = 1. 

(√3/3)² + (√6/3)²  =  3/9 + 6/9

=  (3 + 6)/9

=  9/9

=  1

So, P is on the unit circle. 

Locating a Point on the Unit Circle

Example 3 :

The point P is on the unit circle. Find P(x, y) from the given information. The y-coordinate of P is -1/3 and the x-coordinate is positive.

Solution :

Because the point is on the unit circle, we have 

x² + (-1/3)²  =  1

x² + 1/9  =  1

Subtract 1/9 from each side.

x²  =  1 - 1/9

x²  =  9/9 - 1/9

x²  =  (9 - 1)/9

x²  =  8/9

Take square root on both sides. 

x  =  ± 2√2/3

Because x-coordinate is negative, 

x  =  2√2/3

The point is 

P(2√2/3, -1/3)

Example 4 :

If the the point P(√3/2, k) is on the unit circle in quadrant IV, find P(x, y).   

Solution : 

Because the point is on the unit circle, we have 

(√3/2)² + k²  =  1

3/4 + k²  =  1

Subtract 3/4 from each side.

k²  =  1 - 3/4

k²  =  4/4 - 3/4

k²  =  (4 - 3)/4

k²  =  1/4

Take square root on both sides. 

k  =  ± 1/2

Because the point is in quadrant IV and k is the y-coordinate, the value of k must be negative. 

k = -1/2

The point is 

P(√3/2, -1/2)

Example 5 :

The point P is on the unit circle. Find P(x, y) from the given information. The x-coordinate of P is -2/5 and P lies above the x-axis.

Solution : 

Because the point is on the unit circle, we have 

(-2/5)² + y²  =  1

4/25 + y²  =  1

Subtract 4/25 from each side.

y²  =  1 - 4/25

y²  =  25/25 - 4/25

y²  =  (25 - 4)/25

y²  =  21/25

Take square root on both sides. 

y  =  ± √21/5

Because P lies above the x-axis, y-coordinate must be positive.

y  =  √21/5

The point is 

P(-2/5, √21/5)

Example 6 :

The point P is on the unit circle. Find P(x, y) from the given information. The y-coordinate of P is -1/2 and P lies on the left side of y-axis.

Solution : 

Because the point is on the unit circle, we have 

x² + (-1/2)²  =  1

x² + 1/4  =  1

Subtract 1/4 from each side.

x²  =  1 - 1/4

x²  =  4/4 - 1/4

x²  =  (4 - 1)/4

x²  =  3/4

Take square root on both sides. 

x  =  ± √3/2

Because P lies on the left side of y-axis, x-coordinate must be negative.

x  =  -√3/2

The point is 

P(-√3/2, -1/2)

Related Stuff

1. Terminal Points on the Unit Circle

2. Reference Number on the Unit Circle

3. Using Reference Number to Find terminal Points 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.