UNDERSTANDING EXPONENTS

The picture given below tells us what is exponent and what is base in the given term. 

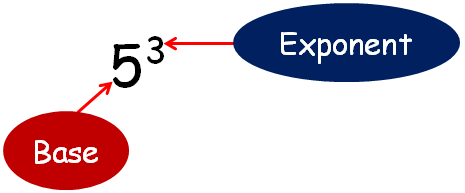
Exponent says that how many times do we have to multiply the base by itself.

For example, let us consider 

2³ =  2 x 2 x 2

In 2³, the exponent is 3. So, we multiply 2 by itself for three times. 

Exponent Rules with Examples

Rule 1 : 

x^m ⋅ xⁿ  =  x^m+n

Example :

3⁴ ⋅ 3⁵  =  3⁴⁺⁵

3⁴ ⋅ 3⁵  =  3⁹

Rule 2 : 

x^m ÷ xⁿ  =  x^m-n

Example :

3⁷ ÷ 3⁵  =  3^7-5

3⁷ ÷ 3⁵  =  3²

Rule 3 : 

(x^m)ⁿ  =  x^mn

Example :

(3²)⁴  =  3⁽²⁾⁽⁴⁾

(3²)⁴  =  3⁸

Rule 4 : 

(xy)^m  =  x^m ⋅ y^m

Example :

(3 ⋅ 5)²  =  3² ⋅ 5²

(3 ⋅ 5)²  =  9 ⋅ 25

(3 ⋅ 5)²  =  225.

Rule 5 : 

(x / y)^m  =  x^m / y^m

Example :

(3 / 5)²  =  3² / 5²

(3 / 5)²  =  9 / 25

Rule 6 : 

x^-m  =  1 / x^m

Example :

3^-2  =  1 / 3²

3^-2  =  1 / 9

Rule 7 : 

x⁰  =  1

Example :

3⁰  =  1

Rule 8 : 

x¹  =  x

Example :

3¹  =  3

Rule 9 : 

x^m/n  =  y -----> x  =  y^n/m

Example :

x^1/2  =  3

x  =  3^2/1

x  =  3²

x  =  9

Rule 10 : 

(x / y)^-m  =  (y / x)^m

Example :

(5 / 3)^-2  =  (3 / 5)²

(5 / 3)^-2  =  3² /  5²

(5 / 3)^-2  =  9 / 25

Rule 11 : 

a^x  =  a^y -----> x  =  y

Example :

3^m  =  3⁵ -----> m  =  5

Rule 12 : 

x^a  =  y^a -----> x  =  y

Example :

k³  =  5³ -----> k  =  5

Note

Many students do not know the difference between 

(-3)²   and   -3²

Order of operations (PEMDAS) dictates that parentheses take precedence.

So, we have

(-3)²  =  (-3) ⋅ (-3)

(-3)²  =  9

Without parentheses, exponents take precedence :

-3²  =  -3 ⋅ 3

-3²  =  -9

The negative is not applied until the exponent operation is carried through. We have to make sure that we understand this. So, we will not make this common mistake. 

Sometimes, the result turns out to be the same, as in. 

(-2)³   and   -2³

We have to make sure why they yield the same result. 

Solved Problems

Problem 1 : 

Find the value of 3⁵. 

Solution : 

=  3⁵

=  3 x 3 x 3 x 3 x 3

=  243

Problem 2 : 

Write the following expression as a power of 5. 

(5³ + 5⁶) / 5⁷

Solution : 

=  (5³ + 5⁶) / 5⁷

=  (5^{3 + 6}) / 5⁷

=  5⁹ / 5⁷

=  5^{9 - 7}

=  5²

Problem 3 : 

If a^-1/2  =  5, then find the value of a. 

Solution : 

a^-1/2  =  5

a  =  5^-2/1

a  =  5^-2

a  =  1/5²

a  =  1/25

Problem 4 : 

If n  =  1² + 1⁴ + 1⁶ + 1⁸ +...............+ 1⁵⁰, then find the value of n. 

Solution : 

1 to the power of anything is equal to 1.

So, we have

1²  =  1

1⁴  =  1

1⁶  =  1

and so on. 

List out all the exponents. 

2, 4, 6, 8, ................ 48, 50

Divide each element by 2.

1, 2, 3, 4, ................ 24, 25

We can clearly see there are 25 terms in the series shown below. 

1² + 1⁴ + 1⁶ + 1⁸ +...............+ 1⁵⁰

Therefore, n is the sum of twenty-five 1's. 

That is, 

n  =  1² + 1⁴ + 1⁶ + 1⁸ +...............+ 1⁵⁰

n  =  25

Problem 5 : 

If 4^{2n + 3}  =  8^{n + 5}, then find the value of n. 

Solution : 

4^{2n + 3}  =  8^{n + 5}

(2²)^{2n + 3}  =  (2³)^{n + 5}

2^{2(2n + 3)}  =  2^{3(n + 5)}

Equate the exponents. 

2(2n + 3)  =  3(n + 5)

4n + 6  =  3n + 15

n  =  9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.