TYPES OF FUNCTIONS PRACTICAL PROBLEMS IN SETS

Problem 1 :

The distance S an object travels under the influence of gravity in time t seconds is given by

S(t) = (1/2) gt² + at + b

where, (g is the acceleration due to gravity), a, b are [constants. Check if the function S(t) is one-one.

Solution :

If for all a₁, a₂ ∈ A, f(a₁) = f(a₂) implies a₁ = a₂ then f is called one – one function.

Let x, y ∈ N, f(x)  =  f(y)

S(x)  =   (1/2) gx² + ax + b  ---(1)

S(y)  =   (1/2) gy² + ay + b  ---(2)

(1)  =  (2)

[(1/2) gx² + ax + b]  =  [(1/2) gy² + ay + b]

[(1/2) gx² + ax + b] - [(1/2) gy² + ay + b]  =  0

(1/2) g(x² - y²) + a(x - y) + b - b  =  0

(x - y) [(1/2) g(x + y) + a]  =  0

x - y = 0

x  =  y

So, it is one to one function.

Problem 2 :

The function ‘t’ which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by

t(C) = F where F = (9/5) C + 32 .

Find, (i) t(0)   (ii) t(28)   (iii) t(-10)

(iv) the value of C when t (C)  =  212

(v) the temperature when the Celsius value is equal to the Farenheit value.

Solution :

Given that, t(C) = (9/5) C + 32 .

(iii) t(-10)

  =  (9/5)(-10) + 32 

  =  -18+32

  =  14° F

(iv) the value of C when t (C)  =  212

(9/5) C + 32  =  212

9C/5  =  212 - 32

9C/5  =  180

C  =  100° C

(v) the temperature when the Celsius value is equal to the Farenheit value.

F  =  C

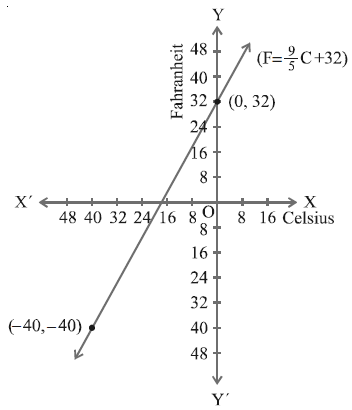
So, the answer is -40°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.