TRIGONOMETRY

Trigonometry is the branch of mathematics that studies the relationships involving lengths of sides and measures of angles of triangles.

It is a useful tool for engineers, scientists, and surveyors and is applied even in seismology and navigation.

Angles

The angle AOB is a measure formed by two rays OA and OB sharing the common point O as shown below. 

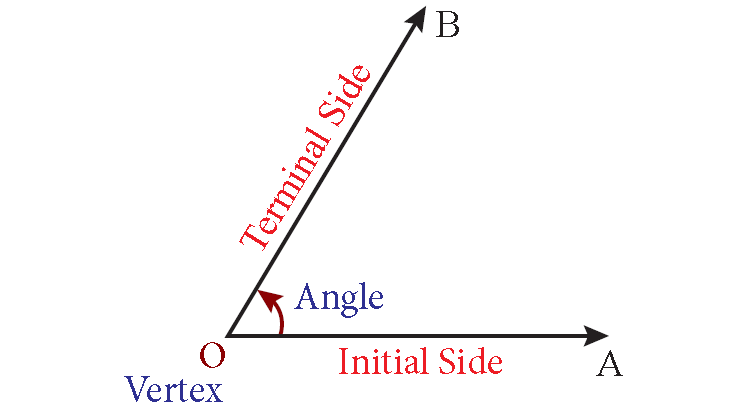
The common point O is called the vertex of the angle.

If we rotate the ray OA about its vertex O and takes the position OB, then OA and OB respectively are called the initial side and the terminal side of the angle produced.

An anticlockwise rotation generates a positive angle (angle with positive sign), while a clockwise rotation generates a negative angle (angle with negative sign).

One full anticlockwise (or clockwise) rotation of OA back to itself is called one complete rotation or revolution.

Degree Measure

The degree is a unit of measurement of angles and is represented by the symbol °.

In degrees, we split up one complete rotation into 360 equal parts and each part is one degree, denoted by 1°. Thus, 1° is 1/360 of one complete rotation.

To measure a fraction of an angle and also for accuracy of measurement of angles, minutes and seconds are introduced. One minute (1') corresponds to 1/60 of a degree and in turn a second (1'') corresponds to 1/60 of a minute (or) 1/3600 of a degree.

Pair of Angles - Classification

We shall classify a pair of angles in the following way for better understanding and usages.

(i) Two angles that have the exact same measure are called congruent angles.

(ii) Two angles that have their measures adding to 90° are called complementary angles.

(iii) Two angles that have their measures adding to 180° are called supplementary angles.

(iv) Two angles between 0° and 360° are conjugate if their sum equals 360°.

Angles in Standard Position

An angle is said to be in standard position, if its vertex is at the origin and its initial side is along the positive x-axis.

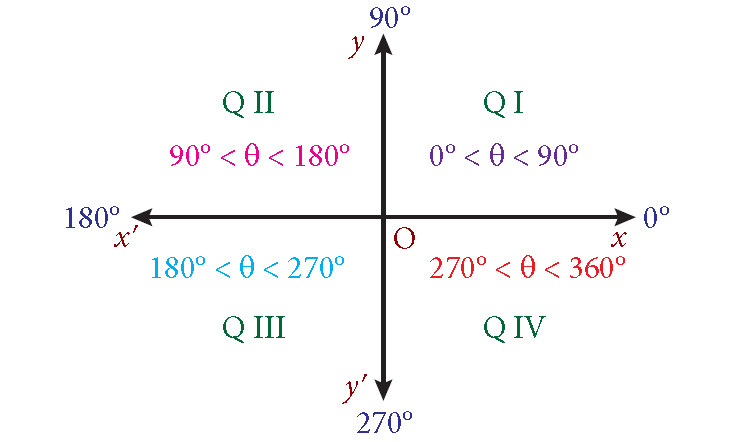
An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant. Similarly, we can define for the other three quadrants.

Angles in standard position having their terminal sides along the x-axis or y-axis are called quadrantal angles.

Thus, 0°, 90°, 180°, 270° and 360° are quadrantal angles.

Coterminal Angles 

One complete rotation of a ray in the anticlockwise direction results in an angle measuring of 360°.

By continuing the anticlockwise rotation, angles larger than 360° can be produced.

If we rotate in clockwise direction, negative angles are produced.

Angles 57°, 417° and −303° have the same initial side and terminal side but with different amount of rotations, such angles are called coterminal angles.

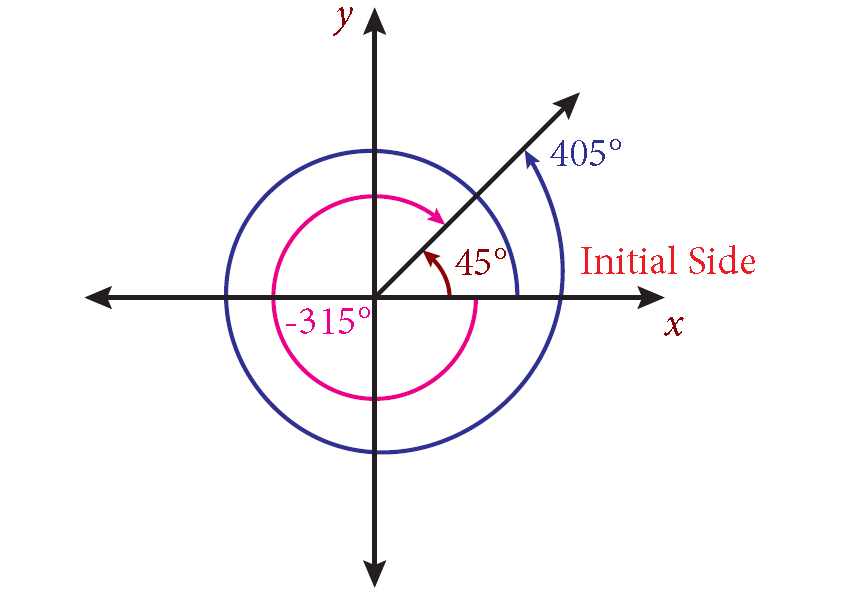
Thus, angles in standard position that have the same terminal sides are coterminal angles . Hence, if α and β are coterminal angles, then

ᵦ  =  α + k(360°), k is an integer

The measurements of coterminal angles differ by an integral multiple of 360°.

For example, 417° and −303° are coterminal because

417° − (−303°)  =  720°  =  2(360°)

Note : 

(i) Observe that 45°, −315° and 405° lie in the first quadrant.

(ii) The following pairs of angles are coterminal angles (30°, 390°) ; (280°, 1000°) and (−85°, 275°).

Radian Measure

The radian measure of an angle is the ratio of the arc length it subtends, to the radius of the circle in which it is the central angle.

Consider a circle of radius r. Let s be the arc length subtending an angle θ at the centre.

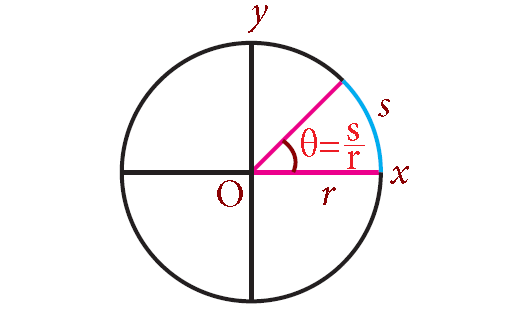
Then, 

θ  =  arc length / radius  =  s/r radians

Hence,

s  =  rθ 

Relationship between Degree and Radian Measures

We have degree and radian units to measure angles. One measuring unit is better than another if it can be defined in a simpler and more intuitive way.

For example, in measuring temperature, Celsius unit is better than Fahrenheit as Celsius was defined using 0° and 100° for freezing and boiling points of water.

Radian measure is better for conversion and calculations. Radian measure is more convenient for analysis whereas degree measure of an angle is more convenient to communicate the concept between people.

Greek Mathematicians observed the relation of π which arises from circumference of a circle and thus, π plays a crucial role in radian measure.

In unit circle, a full rotation corresponds to 360° whereas, a full rotation is related to 2π radians, the circumference of the unit circle.

Thus, we have the following relations :

2π radians  =  360°

Divide each side by 2. 

π radians  =  180° 

Then, 

1 radian  =  (180/π)°  or  1°  =  (π/180) radians

x radians  =  (180x/π)°  or  x°  =  (πx/180) radians

Observe that the scale used in radians is much smaller than the scale in degrees. The smaller scale makes the graphs of trigonometric functions more visible and usable. The above relation gives a way to convert radians into degrees or degrees into radians.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.