TRIGONOMETRY PROBLEMS WITH SOLUTIONS FOR CLASS 11
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Show that
cot(7½°) = √2 + √3 + √4 + √6
Solution :
cot(7½°) :
= cos(7½°) / sin(7½°)
Multiply both numerator and denominator by 2sin(7½°).
= [cos(7½°) ⋅ 2sin(7½°)] / [sin(7½°) ⋅ sin(7½°)]
= [2sin(7½°)cos(7½°)] / sin2(7½°)
= sin(2 ⋅ 7½°) / [1 - cos(2 ⋅ 7½°)]
= sin15° / (1 - cos15°) -----(1)
sin15° = sin(45° - 30°)
= sin45°cos30° - cos45°sin30°
= (1/√2) (√3/2) - (1/√2) (1/2)
= (√3/2√2) - (1/2√2)
= (√3 - 1)/2√2 -----(2)
cos15° = cos(45° - 30°)
= cos45°cos30° + sin45°sin30°
= (1/√2) (√3/2) + (1/√2) (1/2)
= (√3/2√2) + (1/2√2)
= (√3 + 1)/2√2
1 - cos15° :
= 1 - [(√3 + 1)/2√2]
= 1 - (√3 + 1)/2√2]
= [2√2 - (√3 + 1)] / 2√2 -----(2)
(1)----->
= (2)/(3)
= (√3 - 1)/2√2 / {[2√2 - (√3 + 1)]/2√2}
= (√3 - 1) / [2√2 - (√3 + 1)]
Multiply both numerator and denominator by [2√2+(√3+1)].
= (√3 - 1)[2√2 + (√3 + 1)] / [4(2) - (√3 + 1)2]
= (√3 - 1)[2√2 + √3 + 1] / [4(2) - (√3 + 1)2]
= (2√6 + 3 + √3 - 2√2 - √3 - 1)/ [8 - (3 + 1 + 2√3)]
= (2√6 + 2 - 2√2) / [4 - 2√3]
= (√6 + 1 - √2) / [2 - √3]
Multiply both numerator and denominator by (2 + √3).
= (√6 + 1 - √2) (2 + √3) / (2 - √3)(2 + √3)
= (2√6 + 2 - 2√2 + 3√2 + √3 - √6)/(4 - 3)
= √6 + √2 + 2 + √3 / 1
= √6 + √2 + 2 + √3
= √2 + √3 + √4 + √6
Hence proved.
Question 2 :
Prove that
(1 + sec2θ)(1 + sec4θ)..........(1 + sec2nθ) = tan2nθcotθ
Solution :
L.H.S
(1 + sec2θ)(1 + sec4θ).............(1 + sec2nθ)
= (1 + cos2θ)(1 + cos4θ).............(1 + cos2nθ)/(cos2θ cos4θ ......cos2nθ)
= (2cos2θ)(2cos22θ)(2cos24θ) ...........(2cos22n-1θ) / (cos2θ cos4θ ......cos2nθ)
= (2cos2θ) (2cos2θ)(2cos4θ) ...........(2cos22n-1θ)/(cos2nθ)
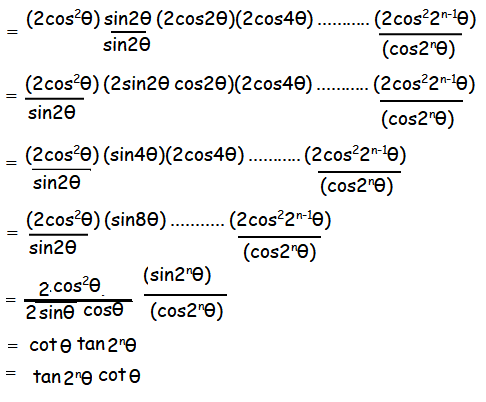
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 40)
Mar 03, 26 06:53 PM
Digital SAT Math Problems and Solutions (Part - 40) -
Digital SAT Math Problems and Solutions (Part - 39)
Mar 03, 26 04:59 PM
Digital SAT Math Problems and Solutions (Part - 39) -
Digital SAT Math Problems and Solutions (Part - 38)
Mar 03, 26 10:05 AM
Digital SAT Math Problems and Solutions (Part - 38)