TRIGONOMETRIC RATIOS WORKSHEET

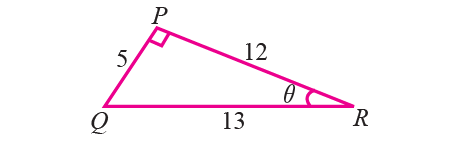
1. In the right triangle shown below, find the six trigonometric ratios of the angle θ.

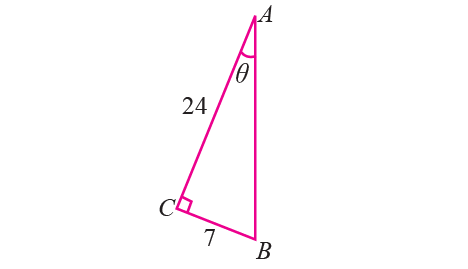
2. In the right triangle shown below, find the six trigonometric ratios of the angle θ.

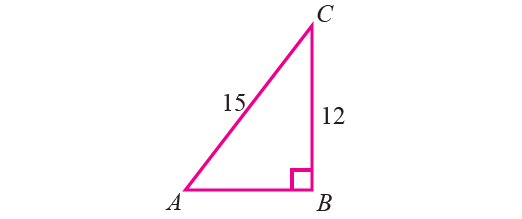
3. In triangle ABC, right angled at B, 15sinA = 12. Find the other five trigonometric ratios of the angle A. Also find the six ratios of the angle C.

4. In the right triangle PQR shown below, find the value of sinθ and cosθ. Using them, find the value of tanθ and cotθ.

5. From the figure given below, find the value of sinθ and cosθ. Using them, find the value of tanθ and cotθ.

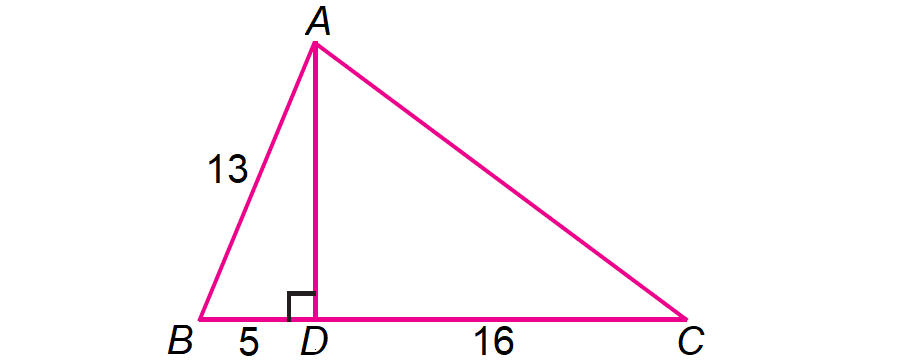
6. In the diagram below, find the values of sinB, secB, cotB, cosC, tanC and cscC.

7. If sinθ = 13/85 and cosθ = 84/85, then find the values of tanθ and cosθ.

Answers

1. Answer :

From the triangle shown above,

opposite side = 5

adjacent side = 12

hypotenuse = 13

Therefore,

2. Answer :

From the right triangle shown above,

AC = 24

BC = 7

By Pythagorean Theorem,

AB² = BC² + CA²

AB² = 7² + 24²

AB² = 49 + 576

AB² = 625

AB² = 25²

AB = 25 

Now, we can use the three sides to find the six trigonometric ratios of angle θ.

Therefore, 

3. Answer :

Given : 15sinA = 12.

Therefore,

opposite side = 12

hypotenuse = 15

Let us consider the right triangle ABC where right angled at B, with    

BC = 12

AC = 15

By Pythagorean theorem,

AC² = AB² + BC²

15² = AB² + 12²

225 = AB² + 144

225 - 144 = AB²

81 = AB²

9² = AB²

9 = AB 

Now, we can use the three sides to find the five trigonometric ratios of angle A and six trigonometric ratios of angle C.

Therefore,

cosA = AB/AC = 9/15 = 3/5

tanA = BC/AB = 12/9 = 4/3

cscA = AC/BC = 15/12 = 5/4

secA = AC/AB = 15/9 = 5/3

cotA = AB/BC = 9/12 = 3/4

sinC = AB/AC = 9/15 = 3/5

cosC = BC/AC = 12/15 = 4/5

tanC = AB/BC = 9/12 = 3/4

cscC = AC/AB = 15/9 = 5/3

secC = AC/BC = 15/12 = 5/4

cotC = BC/AB = 12/9 = 4/3

4. Answer :

From the right triangle shown above,

opposite side = 5

adjacent side = 12

hypotenuse = 13

Therefore,

sinθ = PQ/RQ = 5/13

cosθ = PR/RQ = 12/13

tanθ = sinθ/cosθ = 5/13 ÷ 12/13

tanθ = 5/13 ⋅ 13/12

tanθ = 5/12

cotθ = cosθ/sinθ = 12/13 ÷ 5/13

cotθ = 12/13 ⋅ 13/5

cotθ = 12/5

5. Answer :

From the figure given above, AC = 24 and BC = 7.

By Pythagorean theorem,

AB² = BC² + CA²

AB² = 7² + 24²

AB² = 49 + 576

AB² = 49 + 576

AB² = 625

AB² = 25²

AB = 25 

Now, we can use the three sides to find the six trigonometric ratios of angle θ.

Therefore,

opposite side = 7

adjacent side = 24

hypotenuse = 25

Therefore,

sinθ = BC/AB = 7/25

cosθ = AC/AB = 24/25

tanθ = sinθ/cosθ = 7/25 ÷ 24/25

tanθ = 7/25 ⋅ 25/24

tanθ = 7/24

sinθ = BC/AB = 7/25

cosθ = AC/AB = 24/25

cotθ = cosθ/sinθ = 24/25 ÷ 7/25

cotθ = 24/25 ⋅ 25/7

cotθ = 24/7

6. Answer :

In the right ΔABD, by Pythagorean Theorem,

AB² = AD² + BD²

13² = AD² + 5²

169 = AD² + 25

Subtract 25 from each side.

144 = AD²

12² = AD²

12 = AD

In the right ΔACD, by Pythagorean Theorem,

AC² = AD² + CD²

AC² = 12² + 16²

AC² = 144 + 256

AC² = 400

AC² = 20²

AC = 20

Then,

sinB = opposite side/hypotenuse = AD/AB = 12/13

secB = hypotenuse/adjacent side = AB/BD = 13/5

cotB = adjacent side/opposite side = BD/AD = 5/12

cosC =  adjacent side/hypotenuse 

= CD/AC

= 16/20

= 4/5

tanC = opposite side/adjacent side

= AD/CD

= 12/16

= 3/4

cscC = hypotenuse/opposite side

= AC/AD

= 20/12

= 5/3

7. Answer :

Value of tanθ :

tanθ = sinθ/cosθ

= (13/85)/(84/85)

= (13/85) ⋅ (85/84)

= (13 ⋅ 85)/(85 ⋅ 84)

= 13/84

Value of cotθ :

cotθ = 84/13

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.