TRIGONOMETRIC RATIOS SIN COS AND TAN

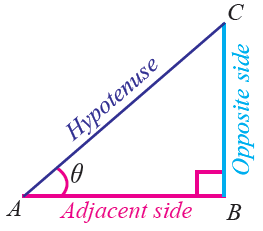
The formulas given below can be used to find the trigonometric ratios sin, cos and tan.

sin θ  =  Opposite side / Hypotenuse

cos θ  =  Adjacent side / Hypotenuse

tan θ  =  Opposite side / Adjacent side

Example 1 :

Find the value of cos C.

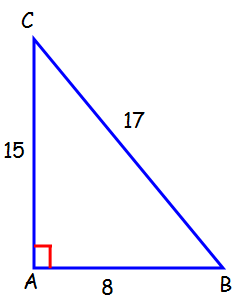
Solution :

90° is at ∠A. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠C is known as opposite side. The remaining side is known as adjacent side.

So, we have

BC  =  Hypotenuse  =  17

AB  =  Opposite side  =  8

AC  =  Adjacent side  =  15

Then, 

cos C  =  Adjacent side / Hypotenuse

cos C  =  AC/BC

cos C  =  15/17

Example 2 :

Find the vale of sin A.

Solution :

90° is at ∠B. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠A is known as opposite side. The remaining side is known as adjacent side.

So, we have

AC  =  Hypotenuse  =  65

BC  =  Opposite side  =  33

AB  =  Adjacent side  =  56

Then, 

sin A  =  Opposite side / Hypotenuse

sin A  =  BC/AC

sin A  =  33/65

Example 3 :

Find the value of tan B.

Solution :

90° is at ∠A. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠B is known as opposite side. The remaining side is known as adjacent side.

So, we have

BC  =  Hypotenuse  =  5

AC  =  Opposite side  =  4

AB  =  Adjacent side  =  3

Then, 

tan B  =  Opposite side / Adjacent side

tan B  =  AC/AB

tan B  =  4/3

Example 4 :

In the triangle below, what is the sum of a and b.

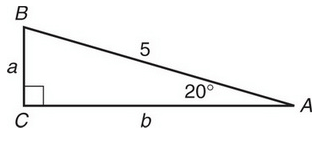
Solution :

Hypotenuse (AB) = 5, Opposite side (BC) = a and adjacent side (AC) = b

a = 1.710 and b = 4.698

a + b = 1.710 + 4.698

= 6.408

So, the sum of a and b is 6.408.

Example 5 :

x + y = 90° and cos y = 7/13, what is the value of sin x ?

Solution :

x + y = 90°

x and y are complementary angles.

y = 90 - x

cos y = cos (90 - x)

Using cofunction identities,

cos y = sin x

cos y = 7/13

sin x = 7/13

Example 6 :

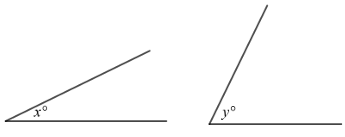
The angles shown above are acute and sin x = cos y. If x = 3z + 5 and y = 2z - 10. What is the value of z ?

a)  15     b)  17     c)  19      d) 37

Solution :

sin x = cos y

sin (3z + 5) = cos (2z - 10)

sin (3z + 5) = sin (90 - (2z - 10))

3z + 5 = 90 - 2z + 10

3z + 5 = 100 - 2z

3z + 2z = 100 - 5

5z = 95

z = 95/5

z = 19

So, the value of z is 19.

Example 7 :

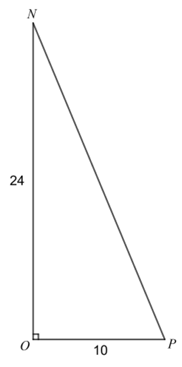
Triangle NOP above, point K (not shown) lies on NP. What is the value of cos (∠KOP) - sin (∠NOK) ?

Solution :

cos (∠KOP) - sin (∠NOK)

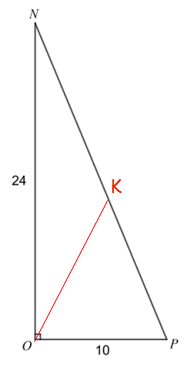
∠KOP  and ∠NOK are complementary angles.

∠KOP  + ∠NOK = 90

∠NOK = 90 - ∠KOP

sin ∠NOK = sin (90 - ∠KOP)

sin ∠NOK = cos ∠KOP ---(1)

Applying (1) in given

Given, cos (∠KOP) - sin (∠NOK) ----(2)

= cos (∠KOP) - cos (∠KOP)

= 0

So, the answer is 0.

Example 8 :

In a right triangle, one angle measure w, where sin w = 5/13. What is cos (90 - w)?

Solution :

sin w = 5/13

cos w = sin (90 - w) similarly, cos (90 - w) = sin w

Then the value of cos (90 - w) = 5/13

Example 9 :

In a triangle above ABC is similar to triangle DEF and ∠B = ∠E. What is the value of tan F ?

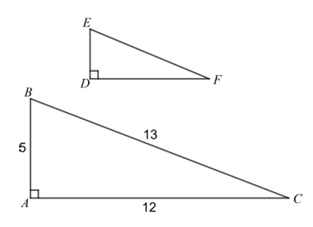
Solution :

If ∠B = ∠E, then ∠F = ∠C

tan C = Opposite side / adjacent side

Opposite side = 5, adjacent side = 12

tan C = 5/12

tan F = 5/12

Example 10 :

Triangle ABC, the measure of ∠C is 90 and AB = 26. If sin  B = 5/13, what is the value of BC ?

Solution :

sin B = 5/13 = Opposite side / Hypotenuse

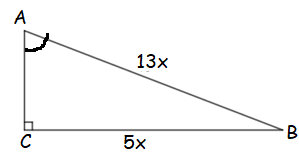
AB = 13x, BC = 5x

AC = √(13x)² - (5x)²

AC = √169x² - 25x²

AC = √144x² 

AC = 12x

AB = 26 = 13x

x = 2

Applying the value of x in 12x, we get

12x = 12(2) ==> 24 cm

Example 11 :

In the triangle given above, find the value tan C.

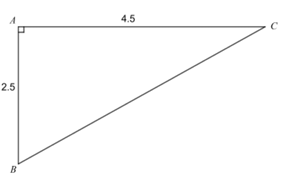
Solution :

tan C = Opposite side / adjacent side

AB = opposite side, AC = adjacent side

tan C = AB/AC

= 2.5/4.5

= 25/45

tan C = 5/9

So, the value of tan C is 5/9.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.