TRIGONOMETRIC RATIOS OF 90 DEGREE MINUS THETA 

Trigonometric ratios of 90 degree minus theta is one of the branches of ASTC formula in trigonometry. 

Trigonometric-ratios of 90 degree minus theta are given below.

sin (90° - θ)  =  cos θ

cos (90° - θ)  =  sin θ

tan (90° - θ)  =  cot θ

csc (90° - θ)  =  sec θ

sec (90° - θ)  =  csc θ

cot (90° - θ)  =  tan θ

Let us see, how the trigonometric ratios of 90 degree minus theta are determined. 

To know that, first we have to understand ASTC formula. 

The ASTC formula can be remembered easily using the following phrases.

"All Sliver Tea Cups" 

or

"All Students Take Calculus"

ASTC formula has been explained clearly in the figure given below.

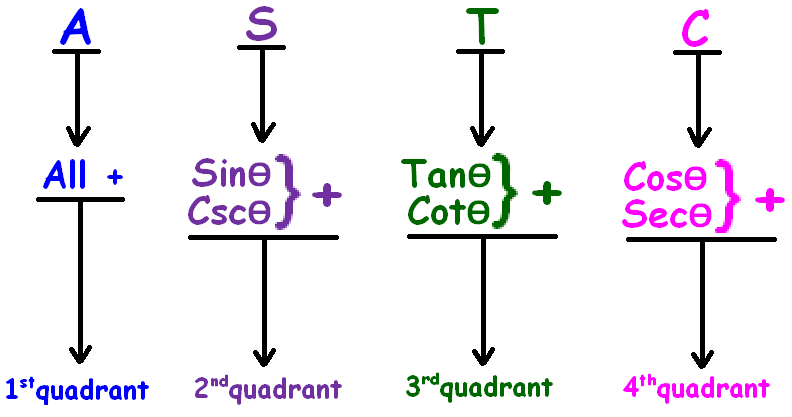
More clearly 

From the above picture, it is very clear that 

(90° - θ) falls in the first quadrant

In the first quadrant (90° - θ), all trigonometric ratios are positive. 

Important Conversions

When we have the angles 90° and 270° in the trigonometric ratios in the form of

(90° + θ)

(90° - θ)

(270° + θ)

(270° - θ)

We have to do the following conversions, 

sin θ <------> cos θ

tan θ <------> cot θ

csc θ <------> sec θ

For example,

sin (270° + θ)  =  - cos θ

cos (90° - θ)  =  sin θ

For the angles 0° or 360° and  180°, we should not make the above conversions. 

Evaluation of Trigonometric Ratios 90 Degree Minus Theta

Problem 1 :

Evaluate :

sin (90° - θ)

Solution :

To evaluate sin (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "sin" will become "cos".

(iii)  In the I^st quadrant, the sign of "sin" is positive. 

Considering the above points, we have 

sin (90° - θ)  =  cos θ

Problem 2 :

Evaluate :

cos (90° - θ)

Solution :

To evaluate cos (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "cos" will become "sin".

(iii)  In the I^st quadrant, the sign of "cos" is positive. 

Considering the above points, we have 

cos (90° - θ)  =  sin θ

Problem 3 :

Evaluate :

tan (90° - θ)

Solution :

To evaluate tan (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "tan" will become "cot".

(iii)  In the I^st quadrant, the sign of "tan" is positive. 

Considering the above points, we have 

tan (90° - θ)  =  cot θ

Problem 4 :

Evaluate :

csc (90° - θ)

Solution :

To evaluate csc (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "csc" will become "sec".

(iii)  In the I^st quadrant, the sign of "csc" is positive. 

Considering the above points, we have 

csc (90° - θ)  =  sec θ

Problem 5 :

Evaluate :

sec (90° - θ)

Solution :

To evaluate sec (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "sec" will become "csc".

(iii)  In the I^st quadrant, the sign of "sec" is positive. 

Considering the above points, we have 

sec (90° - θ)  =  csc θ

Problem 6 :

Evaluate :

cot (90° - θ)

Solution :

To evaluate cot (90° - θ), we have to consider the following important points. 

(i)  (90° - θ) will fall in the I^st quadrant. 

(ii)  When we have 90°, "cot" will become "tan"

(iii)  In the I^st quadrant, the sign of "cot" is positive. 

Considering the above points, we have 

cot (90° - θ)  =  tan θ

Summary (90 Degree Minus Theta)

sin (90° - θ)  =  cos θ

cos (90° - θ)  =  sin θ

tan (90° - θ)  =  cot θ

csc (90° - θ)  =  sec θ

sec (90° - θ)  =  csc θ

cot (90° - θ)  =  tan θ

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.