TRIGONOMETRIC RATIOS OF 270 DEGREE PLUS THETA 

Trigonometric ratios of 270 degree plus theta is one of the branches of ASTC formula in trigonometry. 

Trigonometric-ratios of 270 degree plus theta are given below.

sin (270° + θ)  =  - cos θ

cos (270° + θ)  =  sin θ

tan (270° + θ)  =  - cot θ

csc (270° + θ)  =  - sec θ

sec (270° + θ)  =  cos θ

cot (270° + θ)  =  - tan θ

Let us see, how the trigonometric ratios of 270 degree plus theta are determined. 

To know that, first we have to understand ASTC formula. 

The ASTC formula can be remembered easily using the following phrases.

"All Sliver Tea Cups"

or

"All Students Take Calculus"

ASTC formula has been explained clearly in the figure given below.

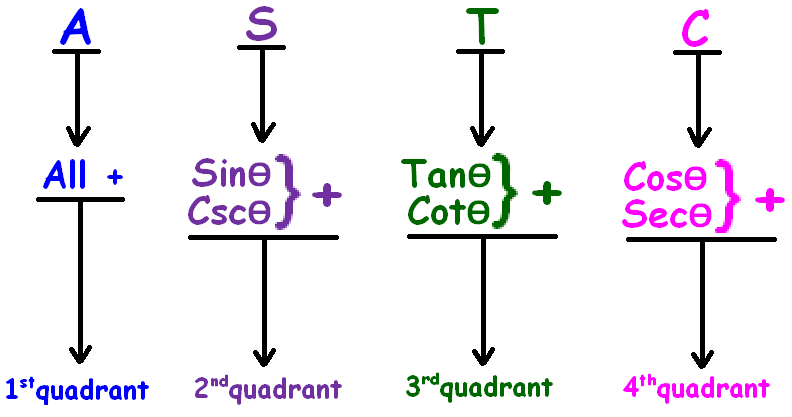
More clearly 

From the above picture, it is very clear that the angle 270 degree plus theta falls in the fourth quadrant.

In the fourth quadrant (270° degree plus theta), cos and sec are positive and other trigonometric ratios are negative.

Important Conversions

When we have the angles 90° and 270° in the trigonometric ratios in the form of

(90° + θ)

(90° - θ)

(270° + θ)

(270° - θ)

We have to do the following conversions, 

sin θ <------> cos θ

tan θ <------> cot θ

csc θ <------> sec θ

For example,

sin (270° + θ)  =  - cos θ

cos (90° - θ)  =  sin θ

For the angles 0° or 360° and  180°, we should not make the above conversions. 

Evaluation of Trigonometric Ratios of 270 Degree Plus Theta

Problem 1 :

Evaluate :

sin (270° + θ)

Solution :

To evaluate sin (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "sin" will become "cos"

(iii)  In the IV^th quadrant, the sign of "sin" is negative. 

Considering the above points, we have 

sin (270° + θ)  =  - cos θ

Problem 2 :

Evaluate :

cos (270° + θ)

Solution :

To evaluate cos (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "cos" will become "sin"

(iii)  In the IV^th quadrant, the sign of "cos" is positive. 

Considering the above points, we have 

cos (270° + θ)  =  sin θ

Problem 3 :

Evaluate :

tan (270° + θ)

Solution :

To evaluate tan (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "tan" will become "cot"

(iii)  In the IV^th quadrant, the sign of "tan" is negative. 

Considering the above points, we have 

tan (270° + θ)  =  - cot θ

Problem 4 :

Evaluate :

csc (270° + θ)

Solution :

To evaluate csc (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "csc" will become "sec"

(iii)  In the IV^th quadrant, the sign of "csc" is negative. 

Considering the above points, we have 

csc (270° + θ)  =  - sec θ

Problem 5 :

Evaluate :

sec (270° + θ)

Solution :

To evaluate sec (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "sec" will become "csc"

(iii)  In the IV^th quadrant, the sign of "sec" is positive. 

Considering the above points, we have 

sec (270° + θ)  =  csc θ

Problem 6 :

Evaluate :

cot (270° + θ)

Solution :

To evaluate cot (270° + θ), we have to consider the following important points. 

(i)  (270° + θ) will fall in the IV^th quadrant. 

(ii)  When we have 270°, "cot" will become "tan"

(iii)  In the IV^th quadrant, the sign of "cot" is negative. 

Considering the above points, we have 

cot (270° + θ)  =  - tan θ

Summary (270 Degree + θ)

sin (270° + θ)  =  - cos θ

cos (270° + θ)  =  sin θ

tan (270° + θ)  =  - cot θ

csc (270° + θ)  =  - sec θ

sec (270° + θ)  =  cos θ

cot (270° + θ)  =  - tan θ

Problem 1 :

Use the double angle formula to find the exact value of the trigonometric function.

sin θ = -7/25 and 3π/2 < θ < 2π. Find cos 2θ.

Solution :

sin θ = -7/25 and 3π/2 < θ < 2π

cos 2θ = 1 - 2sin²θ

= 1 - 2(-7/25)²

= 1 - 2(49/625)

= 1 - (98/625)

= (625 - 98)/625

cos 2θ = 527/625

Problem 2 :

Use the double angle formula to find the exact value of the trigonometric function.

tan θ = 3/4 and π < θ < 3π/2. Find tan 2θ.

Solution :

tan θ = 3/4 and π < θ < 3π/2

tan 2θ = 2 tan θ / (1 - tan² θ)

= 2(3/4) / (1 - (3/4)²)

= (3/2) / (1 - 9/16)

= (3/2) / (7/16)

= 3/2 x (16/7)

= 24/7

Problem 3 :

Evaluate the six trigonometric functions of θ.

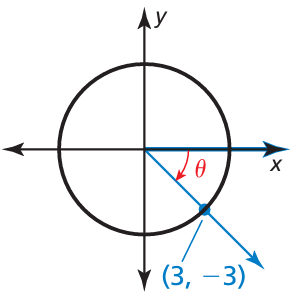
Solution :

Opposite side = -3

Adjacent side = 3

Hypotenuse = √(-3)² + 3²

= √(9 + 9)

= √18

= 3√2

Since the angle lies in the fourth quadrant, the trigonometric ratios cos θ and sec θ only will be positive.

sin θ = Opposite side/Hypotenuse

= -3/3√2

= -1/√2

cos θ = Adjacent side/Hypotenuse

= 3/3√2

= 1/√2

tan θ = Opposite side/Adjacent side

= -3/3

= -1

csc θ = Hypotenuse / Opposite side

= -√2

sec θ = Hypotenuse / Adjacent side

= √2

cot θ = Adjacent side / Opposite side

= -1

Problem 4 :

Use the half angle formula to find the exact value of the trigonometric functions.

cos θ = -15/17 and 180 < θ < 270. Find tan (θ/2)

Since the angle lies in third quadrant, for tan θ and cot θ is positive.

tan (θ/2) = √(1 - cos θ)/(1 + cos θ)

= √(1 - (-15/17))/(1 + (-15/17))

= √(1 + (15/17))/(1 - (15/17))

= √(32/17)/(2/17)

= √(32/17) x (17/2)

= √16

= 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.