TRIGONOMETRIC RATIOS IN SIMILAR RIGHT TRIANGLES

Example 1 :

Find the value of cscE.

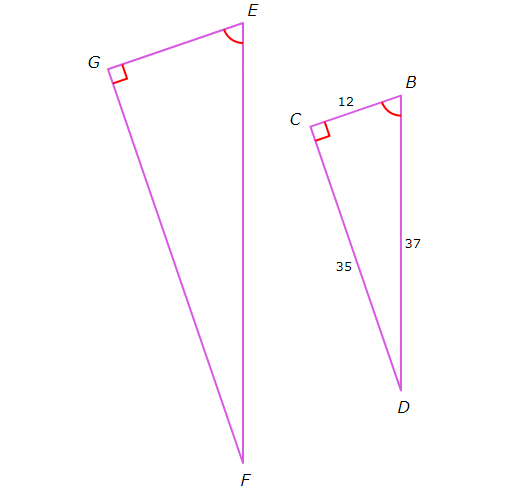
Solution :

In order to find csc E first we have to find the length all sides of triangle GEF.

By observing the above two given triangles, we can prove that the given triangles are similar.

The AA Similarity Theorem states that two triangles are similar if two angles of one triangle are congruent to two angles of the other triangle.

In triangles GEF and BCD,

∠G = ∠C (90 degee)

∠E = ∠B

Therefore, by the AA Similarity Theorem,

△DEF ~ △GIH

So, ratios of corresponding side lengths will be equal.

Then,

EF/BD = GF/CD = GE/BC ----(1)

In triangle EFG,

cscE = Hypotenuse side/ Opposite side

cscE = EF/GF ----(2)

From (2),

EF/BD = GF/CD

EF/GF = BD/CD

EF/GF = 37/35

Substitute 37/35 for EF/GF in (2).

cscE = 37/35

Example 2 :

Find the vale of sec D.

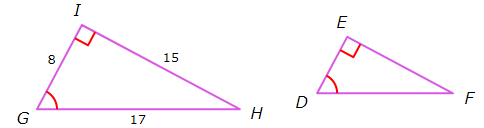
Solution :

By observing the above two triangles, we can prove that the given triangles are similar.

The AA Similarity Theorem states that two triangles are similar, if two angles of one triangle are congruent to two angles of the other triangle.

In triangles GHI and DFE,

∠I = ∠E (90 degree)

∠G = ∠D

Therefore, by the AA Similarity theorem,

△GHI ~ △DFE

So, the ratios of corresponding side lengths will be equal.

Then,

GH/DF = IH/EF = GI/DE ----(1)

secD = Hypotenuse side/Adjacent side

secD = DF/DE ----(2)

From (1),

GH/DF = GI/DE

GH/GI = DF/DE

17/8 = DF/DE

Substitute 17/8 for DF/DE in (2).

secD = 17/8

Example 3 :

Find the value of tan P.

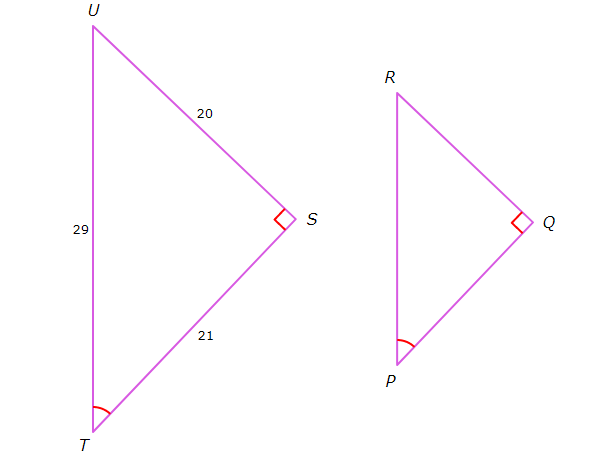
Solution :

By observing the above two given triangles, we can prove that the given triangles are similar.

The AA Similarity Theorem states that two triangles are similar, if two angles of one triangle are congruent to two angles of the other triangle.

In triangles UST and PRQ,

∠S = ∠Q (90 degree)

∠T = ∠P

Therefore, by the AA Similarity theorem,

△UST ~ △PRQ

So, the ratios of corresponding side lengths will be equal.

Then,

UT/RP = US/RQ = TS/PQ ----(1)

tanP = Opposite side/Adjacent side

tan P = RQ/PQ ----(2)

From (1),

US/RQ = TS/PQ

US/TS = RQ/PQ

20/21 = RQ/PQ

Substitute 20/21 for RQ/PQ in (2).

tanP = 20/21

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.