TRIGONOMETRIC RATIOS CSC SEC AND COT

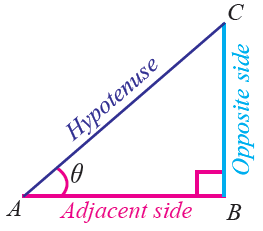
The formulas given below can be used to find the trigonometric ratios csc, sec and cot.

csc θ  =  Hypotenuse / Opposite side

sec θ  =  Hypotenuse / Adjacent side

cot θ  =  Adjacent side / Opposite side

Cofunction identities :

csc (90 - x) = sec x

sec (90 - x) = csc x

cot (90 - x) = tan x

Example 1 :

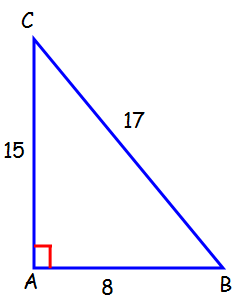
In the right triangle shown below, find the values of csc B, sec B, cot B.

Solution :

90° is at ∠A. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠B is known as opposite side. The remaining side is known as adjacent side.

So, we have

BC  =  Hypotenuse  =  17

AC  =  Opposite side  =  15

AB  =  Adjacent side  =  8

Finding the value of csc B :

csc B  =  Hypotenuse / Opposite side

csc B  =  BC/AC

csc B  =  17/15

Finding the value of sec B :

sec B  =  Hypotenuse / Adjacent side

sec B  =  BC/AB

sec B  =  17/8

Finding the value of cot B :

cot B  =  Adjacent side / Opposite side

cot B  =  AB/AC

cot B  =  8/15

Example 2 :

In the right triangle shown below, find the values of csc A, sec A and cot A.  

Solution :

90° is at ∠B. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠A is known as opposite side. The remaining side is known as adjacent side.

So, we have

AC  =  Hypotenuse  =  65

BC  =  Opposite side  =  33

AB  =  Adjacent side  =  56

Finding the value of csc A :

csc A  =  Hypotenuse / Opposite side

csc A  =  AC/BC

csc A  =  65/33

Finding the value of sec A :

sec A  =  Hypotenuse / Adjacent side

sec A  =  AC/AB

sec A  =  65/56

Finding the value of cot A :

cot A  =  Adjacent side / Opposite side

cot A  =  AB/BC

cot A  =  56/33

Example 3 :

In the right triangle shown below, find the values of csc C, sec C and cot C.  

Solution :

90° is at ∠A. So the side which is opposite to 90° is known as hypotenuse. The side which is opposite to ∠C is known as opposite side. The remaining side is known as adjacent side.

So, we have

BC  =  Hypotenuse  =  5

AB  =  Opposite side  =  3

AC  =  Adjacent side  =  4

Finding the value of csc C :

csc C  =  Hypotenuse / Opposite side

csc C  =  BC/AB

csc C  =  5/3

Finding the value of sec C :

sec C  =  Hypotenuse / Adjacent side

sec C  =  BC/AC

sec C  =  5/4

Finding the value of cot C :

cot C  =  Adjacent side / Opposite side

cot C  =  AC/AB

cot C  =  4/3

Example 4 :

In the right triangle ABC below, the cosine of x is 3/5 . If BC = 12, what is the length of AC and find the value of sec x.

Solution :

cos x = 3/5

Adjacent side (AC) = 3x = 12 ==> then x = 4

and hypotenuse = 5x

5x = 5(4) ==> 20

Opposite side side = √(hypotenuse)² - (Adjacent side)²

= √(5x)² - (3x)²

= √(25x² - 9x²)

= √16x²

Opposite side = 4x

Opposite side = 4(4) ==> 16

Length of AC = 12

sec x = Adjacent side / Hypotenuse

sec x = 12/20

sec x = 3/5

Example 5 :

Let x be the acute angle of a right triangle. Find the values of other 5 trigonometric functions of x, if sec x = 13/5.

Solution :

sec x = 13/5 = Hypotenuse / adjacent side

Hypotenuse = 13x and adjacent side = 5x

Opposite side = √(hypotenuse)² - (Adjacent side)²

= √(13x)² - (5x)²

= √169x² - 25x²

= √144x²

= 12x

sin x = 12x/13x ==> 12/13

cos x = 5x/13x ==> 5/13

tan x = 12x / 5x ==> 12/5

csc x = 13/12

sec x = 13/5

cot x = 5/12

Example 6 :

Using cofunction identities to prove that 

sec² x - cot² (π/2 - x) = 1

Solution :

L.H.S :

sec² x - cot² (π/2 - x) = 1 -----(1)

Using cofunction identities cot (90 - x) = tan x, then 

cot² (90 - x) = tan² x

Applying in (1), we get 

= sec² x - tan² x

= 1

R.H.S

Example 7 :

Using cofunction identities and other identities to simplify the expression

tan(π/2 - x) sin x

Solution :

= tan(π/2 - x) sin x -----(1)

Using cofunction identities,

tan(π/2 - x) = cot x

Applying in (1), we get

= cot x sin x

= (cos x / sin x) (sin x)

= cos x

Example 8 :

Simplify the function

Solution :

Using cofunction identities,

cot (π/2 - 𝜃) = tan 𝜃

sin (-𝜃) = -sin 𝜃

Example 9 :

Solution :

Example 10 :

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.