TRIANGLES AND COORDINATE PROOF
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In geometry, we may already be familiar with two-columns proof, paragraph proofs and flow proofs. A coordinate proof involves placing geometric figures in a coordinate plane. Then, we can use the distance formula and the midpoint formula, as well as postulates and theorems to prove statements about the figures.
Example 1 :
Place a 2-unit by 6-unit rectangle in a coordinate plane.
Solution :
Choose a placement that makes finding distances easy. Here are two possible placements.
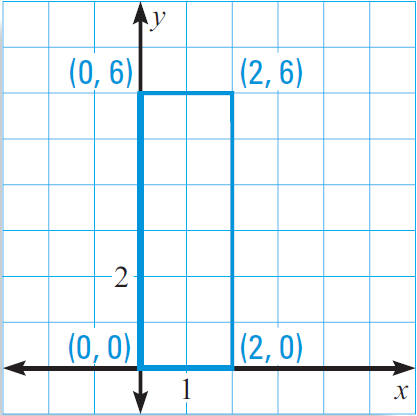
(i) One vertex is at the origin, and three of the vertices have at least one coordinate that is 0.
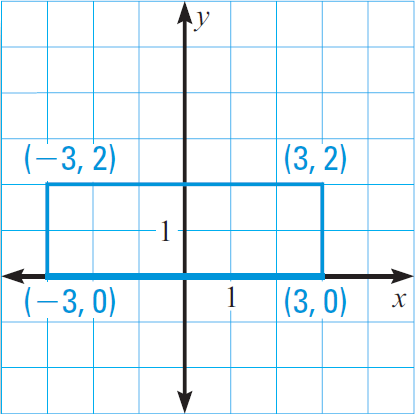
(ii) One side is centered at the origin, and the x-coordinates are opposites.
Note :
Once a figure has been placed in a coordinate plane, you can use the Distance Formula or the Midpoint Formula to measure distances or locate points.
Example 2 :
A right triangle has legs of 5 units and 12 units. Place the triangle in a coordinate plane. Label the coordinates of the vertices and find the length of the hypotenuse.
Solution :
Based on the information given in the question, one possible placement of the triangle is shown below.
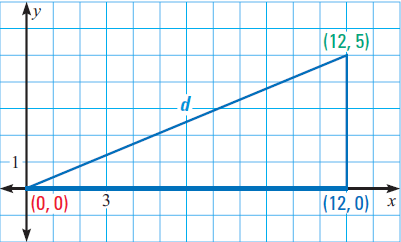
Notice that one leg is vertical and the other leg is horizontal, which assures that the legs meet at right angles. Points on the same vertical segment have the same x-coordinate, and points on the same horizontal segment have the same y-coordinate.
We can use the Distance Formula to find the length of the hypotenuse.
Distance Formula :
d = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (0, 0), (x2, y2) = (12, 5).
d = √[(12 - 0)2 + (5 - 0)2]
Simplify.
d = √(122 + 52)
d = √(144 + 25)
d = √169
d = 13
Example 3 :
In the diagram shown below, ΔMLO ≅ ΔKLO, find the coordinates of point L.
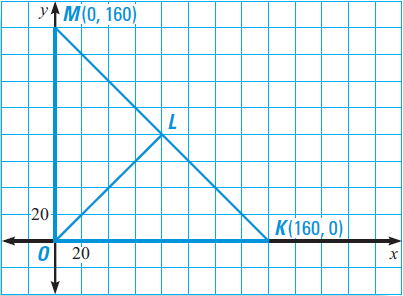
Solution :
Because the triangles are congruent, it follows that
ML ≅ KL
So, point L must be the midpoint of MK. This means, we can use the Midpoint Formula to find the coordinates of point L.
Midpoint Formula :
L(x, y) = [(x1 + x2)/2, (y1 + y2)/2]
Substitute (x1, y1) = K(160, 0), (x2, y2) = M(0, 160).
L(x, y) = [(160 + 0)/2, (0 + 160)/2]
L(x, y) = (160/2, 160/2)
L(x, y) = (80, 80)
The coordinates of the point L are (80, 80).
Example 4 :
In the diagram shown below, prove that ΔOTU ≅ ΔUVO.
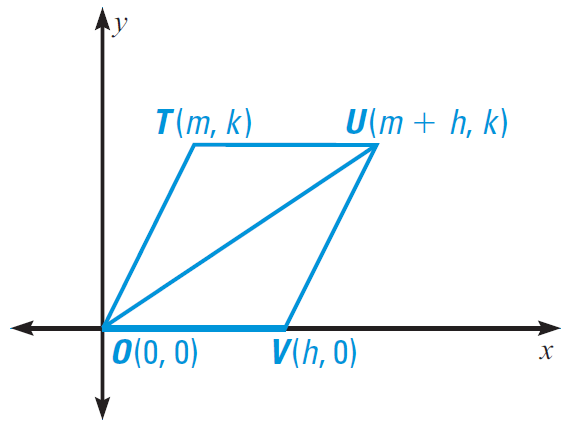
Solution :
Given : Coordinates of figure OTUV.
To prove : ΔOTU ≅ ΔUVO.
Coordinate Proof :
Segments OV and TU have the same length.
Distance Formula :
d = √(x2 - x1)2 + (y2 - y1)2
To find the length of OV, substitute
(x1, y1) = O(0, 0) and (x2, y2) = V(h, 0)
OV = √[(h - 0)2 + (0 - 0)2]
Simplify.
OV = √h2
OV = h
To find the length of TU, substitute
(x1, y1) = T(m, k) and (x2, y2) = U(m + h, k)
TU = √[(m + h - m)2 + (k - k)2]
Simplify.
TU = √h2
TU = h
Horizontal segments TU and OV, each has a slope of 0. This implies that TU and OV are parallel. Segment OU intersects TU and OV to form congruent alternate interior angles ∠TUO ≅ ∠VOU.
Because OU ≅ OU, we can apply the SAS Congruence Postulate to conclude that
ΔOTU ≅ ΔUVO
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

