TRIANGLES AND ANGLES WORKSHEET

Problem 1 :

Prove that the sum of the measures of the interior angles of a triangle is 180°.

Problem 2 :

Can you have a triangle with the following angle measures?

99°, 14° and 67°

Problem 3 :

Find the measures of missing angles in the triangle shown below.

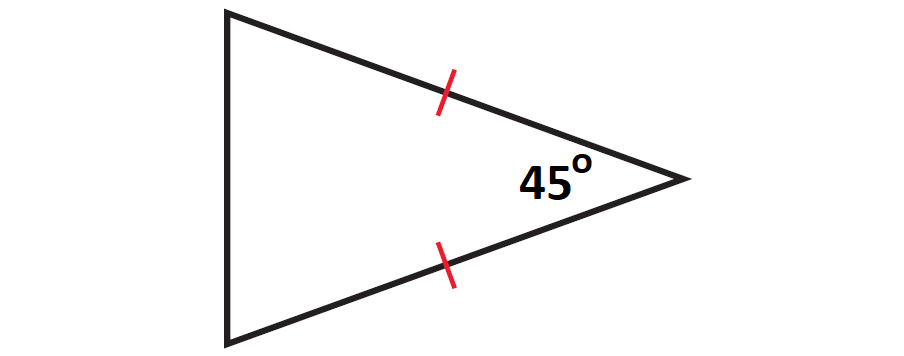
Problem 4 :

The measure of one acute angle of a right triangle is five times the measure of the other acute angle. Find the measure of each acute angle.

Problem 5 :

What is the value of a in the diagram shown below?

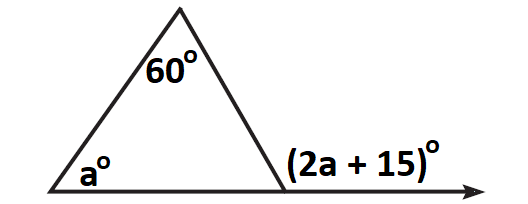
Problem 6 :

Find the measures of all three angles in an isosceles right triangle.

Problem 7 :

In a triangle, the measure of second angle is 1.5 times first angle and the measure of third angle is equal to sum of two times the measure of first angle and the measure of third angle. Find the measures of the three angles of a triangle. 

Answers

1. Answer :

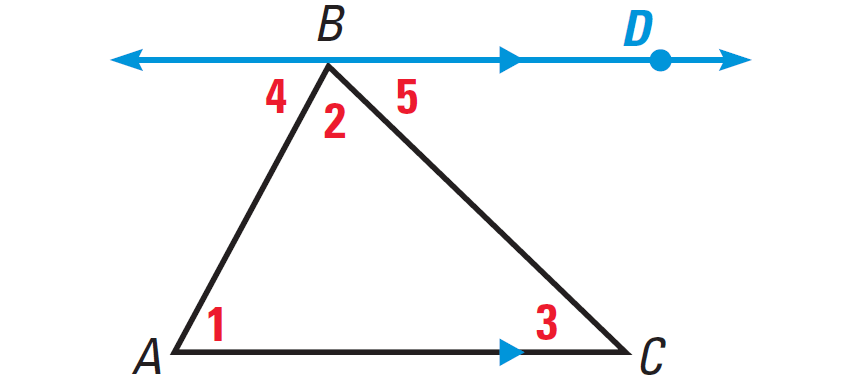
Given :

Triangle ABC

To Prove :

 m∠1 + m∠2 + m∠3 = 180°

Plan for Proof :

By the Parallel Postulate, we can draw an auxiliary line through point B and parallel to AC. Because ∠4, ∠2 and ∠5 form a straight angle, the sum of their measures is 180°.

We also know that ∠1 ≅ ∠4 and ∠3 ≅ ∠5 by the Alternate Interior Angles Theorem.

2. Answer :

We know that sum of the three angles of a triangle is equal to 180°.

Sum of the given angles measures :

99° + 14° + 67° = 180°

Since the sum of the given angle measures is equal 180°, the given three angle measures can be the angles of a triangle.

3. Answer :

In the triangle shown above, two sides are congruent and the angle measures opposite to congruent sides are always congruent.

Let one of the missing angles be x°. Since the two missing angles are congruent, the other missing angle also must be x°.

The diagram shown below illustrates this.

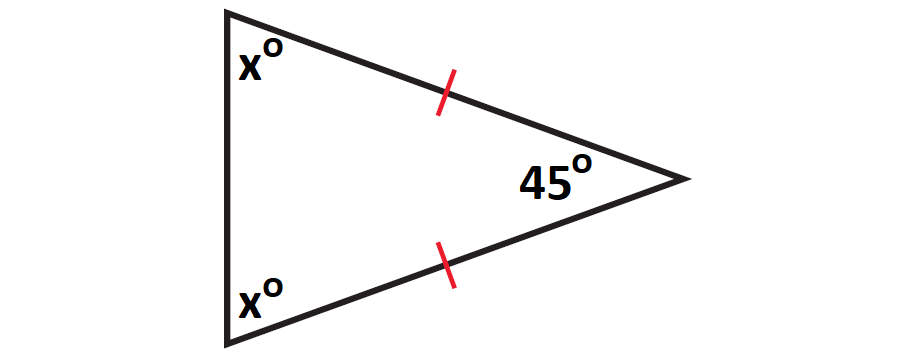
We know that the sum of the angles of a triangle is equal to 180°.

In the triangle shown above,

x° + x° + 45° = 180°

Simplify.

2x° + 45° = 180°

Subtract 45° from both sides.

2x° = 135°

Divide both sides by 2.

x° = 67.5°

So, the measure of each missing angle is 67.5°.

4. Answer :

In the right triangle, let x° be the measure of one of the acute angles.

Then, the measure of the other acute angle is 5x°.

The measures of three angles of the right triangle are x°, 5x° and 90°

sum of the angles of a triangle = 180°

x° + 5x° + 90° = 180°

6x° + 90° = 180°

Subtract 90° from both sides.

6x° = 90°

Divide both sides by 6.

x° = 15°

5x° = 5(15°) = 75°

The measures of two acute angles of the right triangle are 15° and 75°.

5. Answer :

In the triangle shown above, (2a + 15)° is an exterior angle and a° and 60° are remote interior angles to the exterior angle (2a + 10)°.

By Exterior Angle Theorem, the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.

a° + 60° = (2a + 15)°

a + 60 = 2a + 15

Subtract a from both sides.

60 = a + 15

Subtract 15 from both sides.

45 = x

6. Answer :

If a triangle is an isosceles right triangle, one of the angles must be a right angle and two of the sides must be congruent. 

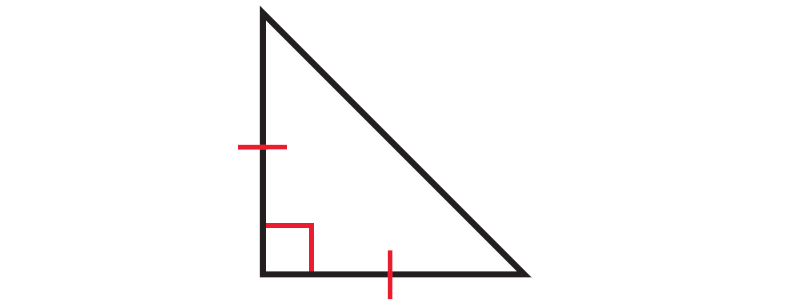
In the triangle shown above, one of the angles is a right angle and two sides are congruent. So, it is an isosceles right triangle.

Angles opposite to congruent sides are always congruent.

Apart from right angle, let x° be one of the two missing angles. Since the two missing angles are congruent, the other missing angle also must be x°.

The diagram shown below illustrates this.

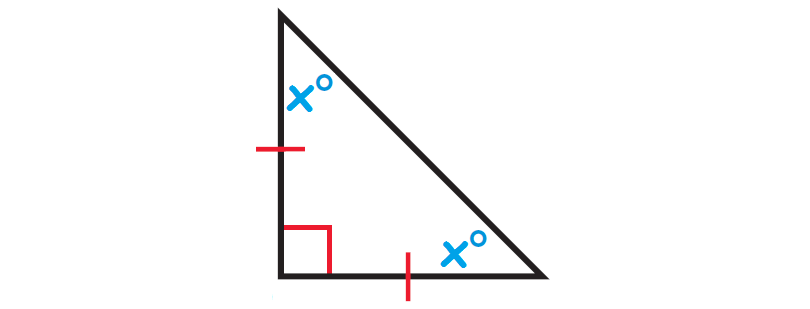
Since one of the angles in the triangle above is a right angle, it is a right triangle.

By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.

x° + x° = 90°

2x = 90

Divide both sides by 2.

x = 45

So, the measure of each missing angle is 45°.

7. Answer :

Let x° be the first angle.

Second angle :

= 1.5x° ----(1)

Third angle :

= two times first angle + second angle

= 2x° + 1.5x°

= 3.5x° ----(2)

Sum of the angles of a triangle = 180°

x° + 1.5x° + 3.5° = 180°

6x° = 180°

Divide both sides by 6.

x° = 30°

Substitute x° = 30° in (1) and (2) to get the measures of second and thoird angles.

second angle = 1.5(30°) = 45°

third angle = 3.5(30°) = 105°

The measures of three angles of the triangle are 30°, 45° and 105°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.