HOW TO CHECK IF THREE POINTS ARE COLLINEAR

To check if the given points are collinear, we may use different concepts. 

• By proving slopes are equal.
• By proving the following condition.

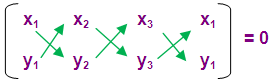
• Finding equation of the line using any two points and applying the another point in that equation and check whether it satisfies

Determine if the following set of points are collinear or not.

Problem 1 :

(4, 3), (1, 2) and (-2, 1)

Solution :

Let A(4, 3), B(1, 2) and C(-2, 1) be the vertices of the triangle.

If the three points are collinear then area of triangle will be zero

x₁ = 4          x₂ = 1         x₃ = -2

y₁ = 3          y₂ = 2         y₃ = 1

=  (1/2)[(8 + 1 – 6) – (3 - 4 + 4)]

=  (1/2)[3 – 3]

=  0

Hence the given points are collinear.

Problem 2 :

(-2, -2), (-6, -2) and (-2, 2)

Solution :

Let A (-2,-2) B (-6,-2) and C (-2,2) are the vertices of the triangle

If the three points are collinear then area of triangle will be zero

x₁ = -2          x₂ = -6         x₃ = -2

y₁ = -2          y₂ = -2         y₃ = 2

  =  (1/2)[(4 - 12 + 4) – (12 + 4 - 4)]

  =  (1/2)[-4 – 12]

  =  (1/2)(-16)

  =  -8  ≠  0

Hence the given points are not collinear.

Problem 3 :

(-3/2, 3) (6, -2) and (-3, 4)

Solution :

Let A (-3/2,3) B (6,-2) and C (-3,4) are the vertices of the triangle

If the three points are collinear then area of triangle will be zero

x₁ = -3/2          x₂ = 6         x₃ = -3

y₁ = 3          y₂ = -2         y₃ = 4

  =  (1/2)[(3 + 24 - 9) – (18 + 6 - 6)]

  =  (1/2)[(27 - 9) - (18)]

  =  (1/2)(18 - 18)

  =  0

Hence the given points are collinear.

In each of the following, find the value of k for which the given points are collinear.

Problem 4 :

(k, -1)  ( 2, 1) and (4, 5)

Solution :

If the given points are collinear then the area of triangle is zero

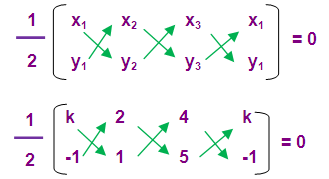
(1/2) [(k + 10 – 4) – (-2 + 4 + 5k)] = 0

[(k + 6) – (2+ 5k)] = 0 x 2

(k + 6 – 2 - 5k) = 0

-4 k + 4 = 0

- 4k = -4

k = (-4)/(-4)

k = 1

Hence, the value of k is 1

Problem 5 :

(2, -5)  ( 3, -4) and (9, k)

Solution :

If the given points are collinear then the area of triangle is zero

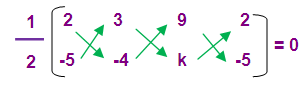
(1/2) [(-8 + 3k – 45) – (-15 - 36 + 2k)]  =  0

[(3k - 53) – (-51+ 2k)]  =  0 x 2

(3k - 53 + 51- 2k)  =  0

 k - 2  =  0

k  =  2

Hence the value of k is 2

Problem 6 :

(k, k)  (2, 3) and (4, -1)

Solution :

If the given points are collinear then the area of triangle is zero

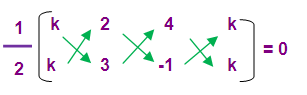
(1/2) [(3k - 2 + 4k) – (2k + 12 - k)]  =  0

[(7k - 2) – (k+12)]  =  0 x 2

(7k - 2 – k - 12)  =  0

 6 k - 14  =  0

6k  =  14

K  =  14/6  

K  = 7/3

Hence the value of k is 7/3.

Problem 7 :

Plot the points A(5, 3), B(−2, 3),D(5, −4) which are three vertices of a square ABCD. Hence find the co-ordinates of C. Also find the area of it.

Solution :

By ploting the given three points, we know that (5, -4) and the required point C should be collinear.

The distance between the point (-2, 3) and (5, 3) is 7 units.

By choosing the point with the same distance of 7 units, opposite to (5, -4) we get (-2, -4)

Area of square = a²

Side length = 7 units

= 7²

= 49 square units.

Problem 8 :

Show that the points (-2, 5), (6, -1) and (2, 2) are collinear.

Solution :

Let the given points be A (-2, 5), B (6, -1) and C (2, 2)

Slope = (y₂ - y₁) / (x₂ - x₁)

Slope of AB = (-1 - 5) / (6 - (-2))

= -6/(6 + 2)

= -6/8

= -3/4

Slope of AC = (2 - 5)/ (2 - (-2))

= -3/(2 + 2)

= -3/4

Since slopes are equal, the points are collinear.

Problem 9 :

(2, 1) is the point of intersection of two lines.

a) x - y - 3 = 0, 3x - y - 7 = 0

b) x + y = 3, 3x + y = 7     c) 3x + y = 3, x + y = 7

d)  x + 3y - 3 = 0, x - y - 7 = 0

Solution :

Option a :

x - y - 3 = 0, 3x - y - 7 = 0

Check if the point (2, 1) lies on the above line,

Option b :

x + y = 3, 3x + y = 7 

Check if the point (2, 1) lies on the above line,

So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.