FINDING UNKNOWN VERTICES WHEN AREA OF TRIANGLE IS GIVEN
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Vertices of the triangle taken in order and their areas are given below. In each of the following find the value of a.
Problem 1 :
Whose vertices are (0, 0), (4, a) and (6, 4) and its area is 17 sq.units
Solution :
Area of the triangle = 17 square units
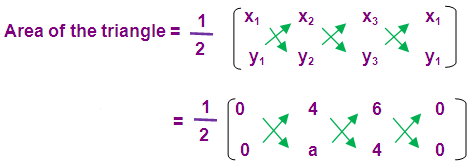
(1/2)[(0 + 16 + 0) – (0 + 6a + 0)] = 17
(1/2)(16 – 6 a) = 17
8 - 3a = 17
-3a = 9
a = -3
So, the value of a is -3.
Problem 2 :
The vertices are (a, a) , (4 , 5) and ( 6 , -1) and its area is 9 sq. units
Solution :
Area of the triangle = 9 square units
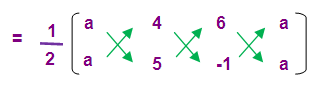
(1/2)[(5a - 4 + 6a) – (4a + 30 - a)]
(1/2)[(11a – 4) – ( 3a+30)] = 9
(1/2)[11a – 4 – 3a - 30] = 9
(1/2)[8a – 34] = 9
4a – 17 = 9
4a = 26
a = 26/4
a = 13/2
So, the value of a is 13/2.
Problem 3 :
The vertices are (a, -3),(3, a) and (-1, 5) and its area is 12 sq.units
Solution :
Area of the triangle = 12 square units
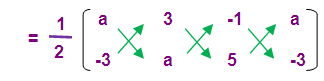
(1/2)[(a2 + 15 + 3) – (-9 - a + 5a)] = 12
(1/2)[(a2 + 18 ) – (-9 + 4a)] = 12
[a2 + 18 + 9 - 4a] = 12 x 2
a2 - 4a + 27 = 24
a2 - 4a + 27 - 24 = 0
a2 - 4a + 3 = 0
(a - 1)(a - 3) = 0
a = 1, 3
So, the values of a are 1 and 3.
Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’.
Problem 4 :
The vertices are (0, 0), (p, 8), (6, 2) and has the area of 20 square units.
Solution :
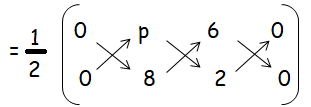
Area of triangle = (1/2) [(0 + 2p + 0) - (0 + 48 + 0)]
(1/2) [(0 + 2p + 0) - (0 + 48 + 0)] = 20 square units
(1/2)(2p - 48) = 20
2p - 48 = 20(2)
2p - 48 = 40
2p = 40 + 48
p = 88/2
p = 44
So, the value of p is 44.
Problem 5 :
The vertices are (p, p), (5, 6), (5, –2) and has the area of 32 square units.
Solution :
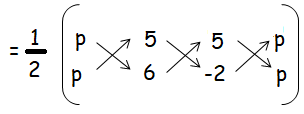
Area of triangle = (1/2) [(6p - 10 + 5p) - (5p + 30 - 2p)]
(1/2) [(6p - 10 + 5p - 5p - 30 + 2p] = 32 square units
(1/2) (8p - 40) = 32 square units
(8p - 40) = 32(2)
8p - 40 = 64
8p = 64 + 40
8p = 104
p = 104/8
p = 13
So, the value of p is 13.
Problem 6 :
The area of triangle formed by the points (−5,0) , (0,−5) and (5,0) is
(A) 0 sq.units (B) 25 sq.units (C) 5 sq.units
(D) none of these
Solution :
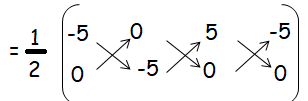
= (1/2) [(25 + 0 + 0) - (0 - 25 - 0)]
= (1/2) [25 - (- 25)]
= (1/2) (25 + 25)
= (1/2) x 50
= 25 square units.
So, the required area of triangle is 25 square units.
Problem 7 :
If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is
(A) 3 (B) 6 (C) 9 (D) 12
Solution :
Since these points are collinear, then the area of triangle joining these three points will be 0.
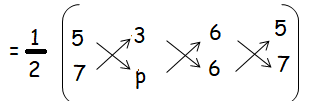
0 = (1/2) [(5p + 18 + 42) - (21 + 6p + 30)]
0 = (1/2) [(5p + 60) - (51 + 6p)]
0 = (1/2) [5p + 60 - 51 - 6p]
0 = (1/2) [-p + 9]
-p + 9 = 0
p = 9
So, the value of p is 9.
In each of the following, find the value of ‘a’ for which the given points are collinear.
Problem 8 :
(2, 3), (4, a) and (6, –3)
Solution :
When the points are collinear, the area created by these points will be 0.
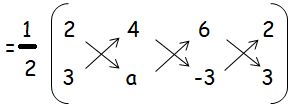
= (1/2)[(2a - 12 + 18) - (12 + 6a - 6)]
= (1/2)[(2a + 6) - (6 + 6a)]
= (1/2)[2a + 6 - 6 - 6a]
= (1/2)[-4a]
4a = 0
a = 0
So, the required value of a is 0.
Problem 9 :
(a, 2 – 2a), (–a + 1, 2a) and (–4 – a, 6 – 2a)
Solution :
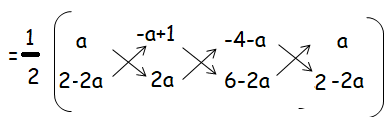
= (1/2){[2a2 + (-a + 1)(6 - 2a) + (-4 - a) (2 - 2a)] - [(2 - 2a)(-a + 1) + 2a(-4 - a) + a(6 - 2a)]
= (1/2){ [2a2 -6a + 2a2 + 6 - 2a - 8 + 8a - 2a + 2a2] -
[-2a + 2 + 2a2 - 2a - 8a - 2a2 + 6a - 2a2] }
= (1/2){ [6a2 - 2a - 2] - (-2a2 - 6a + 2)] }
0 = (1/2){6a2 - 2a - 2 + 2a2 + 6a - 2}
8a2 - 4a - 4 = 0
Dividing by 4, we get
2a2 - a - 1 = 0
(2a + 1)(a - 1) = 0
a = -1/2 and a = 1
so, the possible values of a are 1 and -1/2.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


