TRANSLATIONS USING VECTORS WORKSHEET

Problem 1 :

The diagram below shows a vector. 

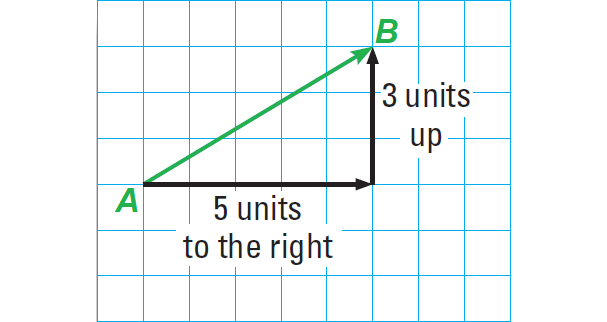
a. Name the vector.

b. Write the initial point and terminal point of the vector. 

b. Write the horizontal and Vertical components of the vector. 

c. Write the component form of the vector.  

Problem 2 :

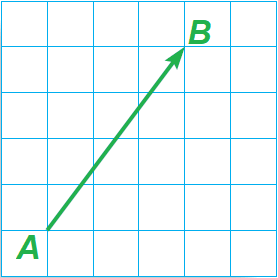
In the diagram shown below, name the vector and write its component form. 

Problem 3 :

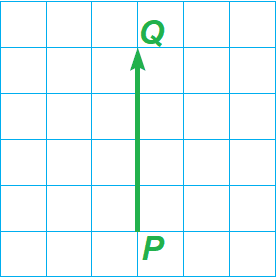
In the diagram shown below, name the vector and write its component form. 

Problem 4 :

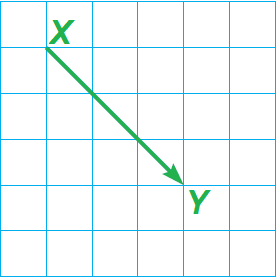
In the diagram shown below, name the vector and write its component form. 

Problem 5 :

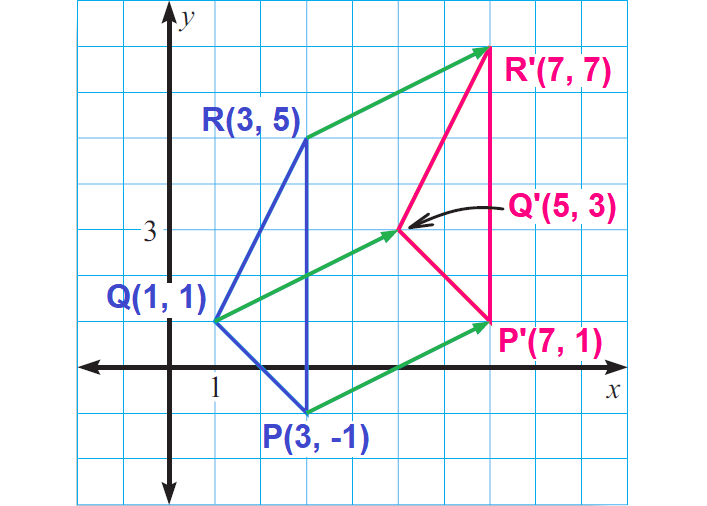
The component form of the vector XY is 〈4, 2〉. Use the vector XY to translate the triangle whose vertices are

P(3, -1), Q (1, 1) and R(3, 5)

Problem 6 :

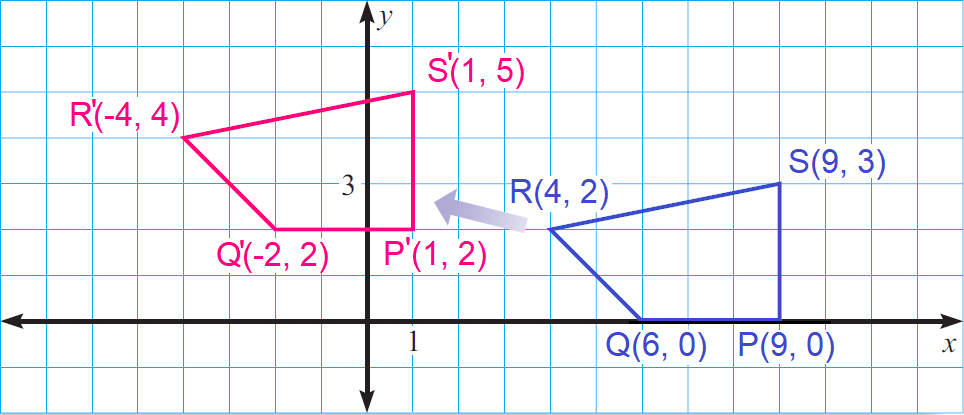
In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.

Problem 7 :

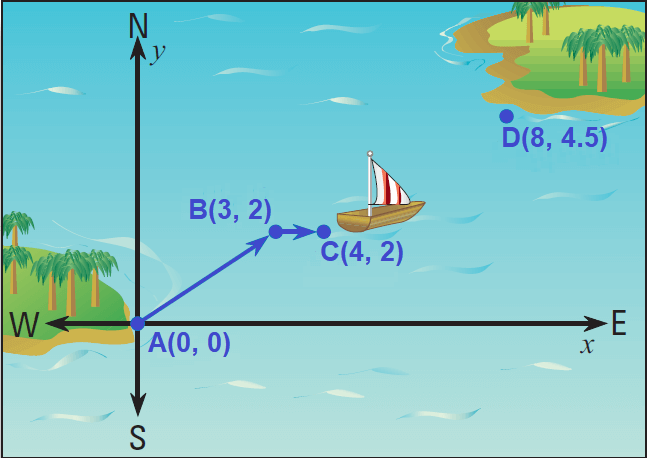
A boat travels a straight path between two islands, A and D. When the boat is 3 miles east and 2 miles north of its starting point it encounters a storm at point B. The storm pushes the boat off course to point C, as shown below.

Answers

Problem 1 :

The diagram below shows a vector. 

a. Name the vector.

b. Write the initial point and terminal point of the vector. 

b. Write the horizontal and Vertical components of the vector. 

c. Write the component form of the vector. 

Solution :

Part (a) :

The vector is AB.

Part (b) :

The initial point or starting point of the vector is A and the terminal point or ending point is B.

Part (c) :

The horizontal component of the vector AB is 5 and the vertical component is 3. 

Part (d) :

The component form of a vector combines the horizontal and vertical components.

So, the component form of AB is

〈5, 3〉

Problem 2 : 

In the diagram shown below, name the vector and write its component form. 

Solution :

The vector is AB.

To move from the initial point A to the terminal point B, we have to move 3 units to the right and 4 units up.

So, the component form is

〈3, 4〉

Problem 3 : 

In the diagram shown below, name the vector and write its component form. 

Solution :

The vector is PQ.

To move from the initial point P to the terminal point Q, we have to move 0 units to the right and 4 units up.

So, the component form is

〈0, 4〉

Problem 4 : 

In the diagram shown below, name the vector and write its component form. 

Solution :

The vector is XY.

To move from the initial point P to the terminal point Q, we have to move 3 units to the right and 3 units down.

So, the component form is

〈3, -3〉

Problem 5 : 

The component form of the vector XY is 〈4, 2〉. Use the vector XY to translate the triangle whose vertices are

P(3, -1), Q (1, 1) and R(3, 5)

Solution :

First graph ΔPQR. The component form of the vector XY is 〈4, 2〉, so the image vertices should all be 4 units to the right and 2 units up from the preimage vertices.

That is, 

P(3, 1) ----> (3 + 4, - 1 + 2) ----> P'(7, 1)

Q(1, 1) ----> (1 + 4, 1 + 2) ----> P'(5, 3)

R(3, 5) ----> (3 + 4, 5 + 2) ----> P'(7, 7)

Label the image vertices as P'(7, 1), Q'(5, 3), and R'(7, 7). Then, using a straightedge, draw ΔP'Q'R'.

Notice that the vectors drawn from preimage to image vertices are parallel.

Problem 6 : 

In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.

Solution :

Choose any vertex and its image, say R and R'. To move from R to R', we have to move 8 units to the left and 2 units up.

So, the component form of the vector is

〈-8, 2〉

Problem 7 : 

A boat travels a straight path between two islands, A and D. When the boat is 3 miles east and 2 miles north of its starting point it encounters a storm at point B. The storm pushes the boat off course to point C, as shown below.

a. Write the component forms of the two vectors shown in the diagram.

b. The final destination is 8 miles east and 4.5 miles north of the starting point. Write the component form of the vector that describes the path the boat can follow to arrive at its destination.

Solution :

Part (a) :

The component form of the vector from A(0, 0) to B(3, 2) is

vector AB  =  〈3 - 0, 2 - 0〉  =  〈3, 2〉

The component form of the vector from B(3, 2) to C(4, 2) is

vector BC  =  〈4 - 3, 2 - 2〉  =  〈1, 0〉

Part (b) :

The boat needs to travel from its current position, point C, to the island, point D. To find the component form of the vector from C(4, 2) to D(8, 4.5), subtract the corresponding coordinates :

vector CD  =  〈8 - 4, 4.5 - 2〉  =  〈4, 2.5〉

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.