TRANSLATIONS AND VECTORS

Using Properties of Translations

A translation is a transformation that maps every two points A and B in the plane to points A' and B', so that the following properties are true.

1. AA' = BB'.

2. AA' ∥ BB' or AA' and BB' are collinear.

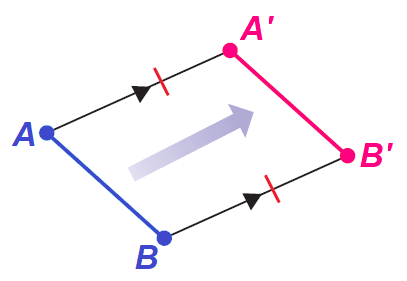
Translation Theorem

A translation is an isometry.

Translation Theorem can be proven as follows.

Given : AA' = BB', AA' ∥ BB'.

Prove : AB = A'B'.

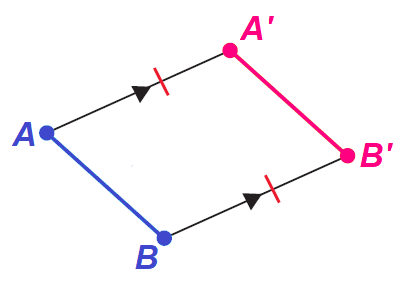
Proof :

The quadrilateral AA'B'B has a pair of opposite sides that are congruent and parallel, which implies AA'B'B is a parallelogram.

From this we can conclude

AB = A'B'

We can find the image of a translation by gliding a figure in the plane. Another way to find the image of a translation is to complete one reflection after another in two parallel lines, as shown.

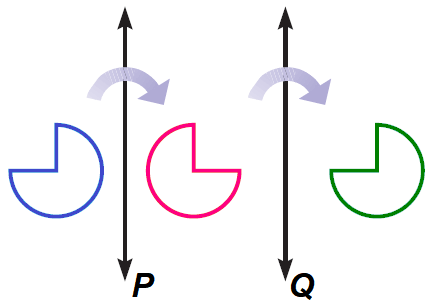
Translations in Parallel Lines -Theorem

If lines k and m are parallel, then a reflection in line m followed by a reflection in line n is a translation. If P" is the image P, then the following is true.

1. PP" is perpendicular to k and m.

2. PP" = 2d, where d is the distance between k and m.

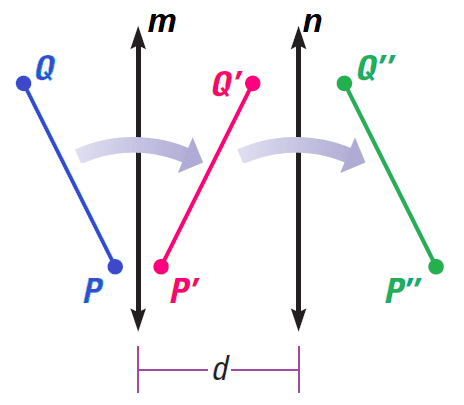
Example 1 :

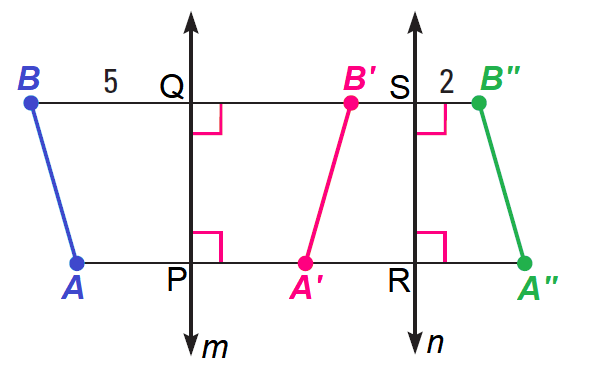
In the diagram shown above, a reflection in line m maps AB to A'B', a reflection in line n maps A"B" to A"B" and

m ∥ n, HB = 5 and DH" = 2

a. Name some congruent segments.

b. Does AC = BD? Explain.

c. What is the length of GG"?

Solution (a) :

Here are some sets of congruent segments :

AB, A'B' and A"B"

BQ and B'Q

B'S and B"S

Solution (b) :

Yes, PR = QS because PR and QS are opposite sides of a rectangle.

Solution (c) :

Because, AA" = BB", the length of AA" is

= 5 + 5 + 2 + 2

= 14 units

Translations in a Coordinate Plane

Translations in a coordinate plane can be described by the following coordinate notation :

(x, y) ----> (x + a, y + b)

where a and b are constants. Each point shifts a units horizontally and b units vertically.

Example 2 :

Describe the translation in the coordinate plane shown below.

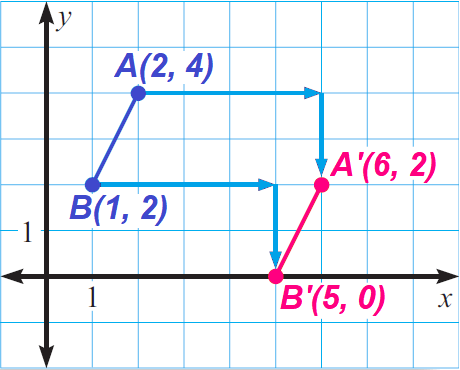
Solution :

In the coordinate plane shown above, the translation is

(x, y) ----> (x + 4, y - 2)

That is, the translation in the coordinate plane above shifts each point 4 units to the right and 2 units down. 

Translations and Vectors

Another way to describe a translation is by using a vector. A vector is a quantity that has both direction and magnitude, or size, and is represented by an arrow drawn between two points.

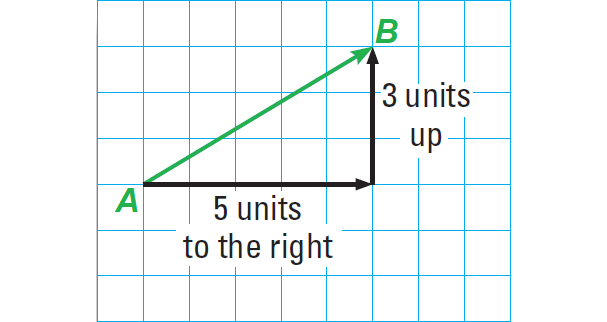
The diagram above shows a vector. The initial point or starting point of the vector is A and the terminal point or ending point is B. The vector is named AB which is read as "vector AB". The horizontal component of AB is 5 and the vertical component of AB is 3.

The component form of a vector combines the horizontal and vertical components. So, the component form of AB is

〈5, 3〉

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.