TRANSFORMATIONS : HORIZONTAL STRETCH, COMPRESSION AND REFLECTION

Doing stretches, compressions and reflections horizontally are different types of transformations of functions. 

To make the students to understand the stuff "Horizontal stretches, compressions and reflections",  we have explained the rule that we have to apply to make horizontal stretch, compression and reflection in a function.

Horizontal Stretches and Compressions

Let y = f(x) be a function.

In the above function, if we want to do horizontal expansion or compression by a factor of "k", at every where of the function, "x" co-ordinate has to be multiplied by the factor "k". Then, we get the new function 

y  =  f(kx)  

The graph of y = f(kx) can be obtained by expanding or compressing the graph of  y = f(x) horizontally by the factor "k".

It can be done by using the rule given below.

Note :

Stretch and expansion mean the same thing. 

Horizontal Stretch - Example

Once students understand the above mentioned rule which they have to apply for horizontal stretch or compression, they can easily do this kind of transformations of functions.

Let us consider the following example to have better understanding of horizontal expansion. 

Question :

Perform the following transformation to the function        y = √x.

               "an horizontal strech by a factor 0.5"

And also write the formula that gives the requested transformation and draw the graph of both the given function and the transformed function

Solution :

Step 1 :

Since we do horizontal stretch by the factor "0.5", we have to replace  "x" by "0.5x" in the given function y = √x.

Step 2 :

So, the formula that gives the requested transformation is    

y  =  √0.5x 

Step 3 :

The graph y =  √0.5x  can be obtained by strtching the graph of the function y = √x horizontally by the factor 0.5. 

(x, y) -------> (0.5x, y)

Step 4 :

The graph of the original function (given function)

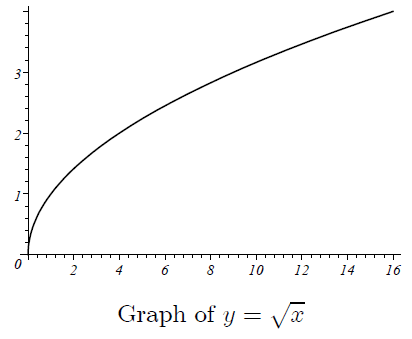
Step 5 :

The graph of the function in which horizontal stretch made by the factor "0.5".

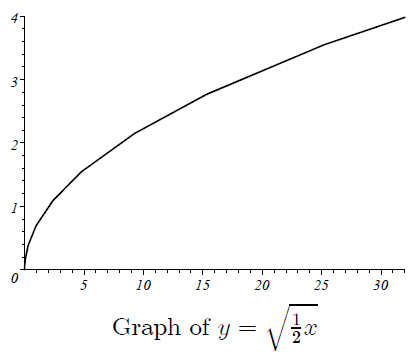
How to sketch the graph of the function which is  horizontally stretched or compressed ? 

Let "y = f(x)" be the given function and (x , y) by any point on the graph of the function y = f(x).

If we want to perform horizontal stretch in the graph of the function  y = f(x) by the factor "0.5", we have to write the point (x , y) as (0.5x ,  y).

That is, "x" co-ordinate of each and every point to be multiplied by the factor 0.5. 

Therefore, any point on the horizontally stretched graph will be in the form of   (0.5x , y)

So, each and every point to be changed according to (0.5x , y) and plot them on the graph.

After having plotted the points, if we connect all the points, we will get the horizontally stretched graph.

The same procedure to be followed for horizontal compression.

Reflections

Let y = f(x) be a function.

The graph of the function f(x) can be reflected about x- axis or y-axis or the line y = x or the line y = -x or the origin using the rules given below. 

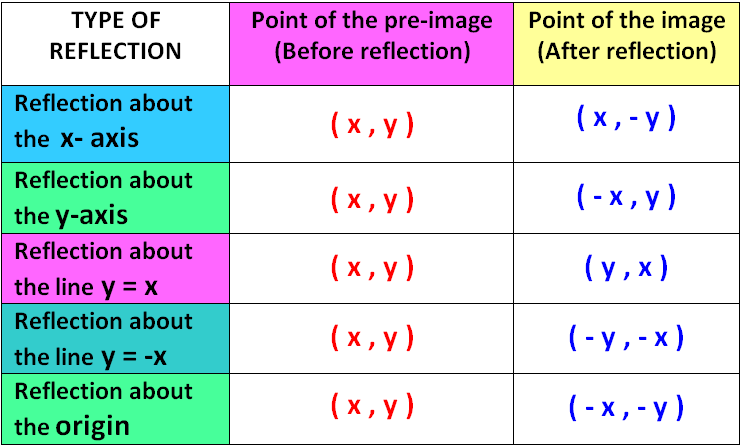
Based on the rules given above, the images and their reflections about x- axis and y-axis and the line y = x are given below.

Reflection about x - axis :

Reflection about y - axis :

Reflection about the line y = x :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.