TRANSFORMATION OF GRAPHS OF MODULUS FUNCTION

Here we are going to see, transformation of graphs of modulus function.

Reflection :

A reflection is the mirror image of the graph where line l is the mirror of the reflection.

(i) The graph y = −f(x) is the reflection of the graph of f about the x-axis.

(ii) The graph y = f(−x) is the reflection of the graph of f about the y-axis.

(iii) The graph of y = f⁻¹(x) is the reflection of the graph of f in y = x.

Translation :

A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs.

The graph of

y = f(x + c), c > 0 causes the shift to the left.

y = f(x − c), c > 0 causes the shift to the right.

y = f(x) + d, d > 0 causes the shift to the upward.

y = f(x) − d, d > 0 causes the shift to the downward.

Dilation :

Dilation is also a transformation which causes the curve stretches (expands) or compresses (contracts). Multiplying a function by a positive constant vertically stretches or compresses its graph; that is, the graph moves away from x-axis or towards x-axis. 

If the positive constant is greater than one, the graph moves away from the x-axis. If the positive constant is less than one, the graph moves towards the x-axis.

Practice Question

Problem 1 :

From the curve y = |x|, draw

(i) y = |x − 1| + 1

(ii) y = |x + 1| − 1

(iii) y = |x + 2| − 3

Solution :

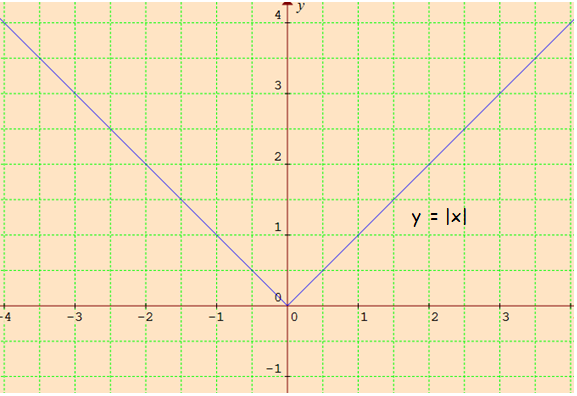
First let us draw the graph of y = |x|, for any negative values of x, we will get positive values of y.

So, the graph will be

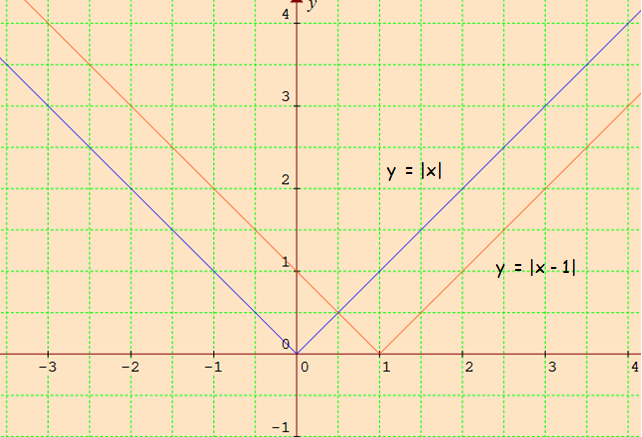
(i) y = |x − 1| + 1

First 1 is subtracted from x in the modulus function, so we have to move the curve 1 unit to the right side.

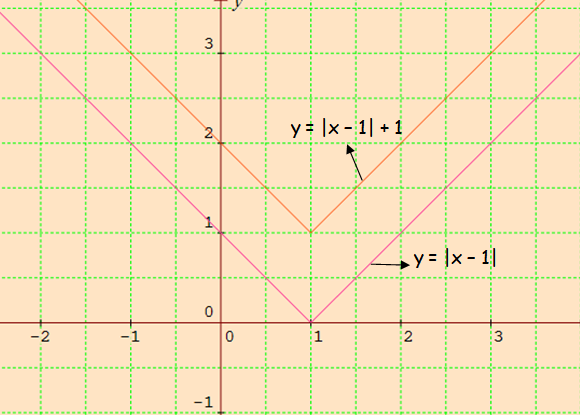
1 is added to |x - 1|, so we have to move the graph of y = |x - 1| 1 unit upward direction.,

Problem 2 :

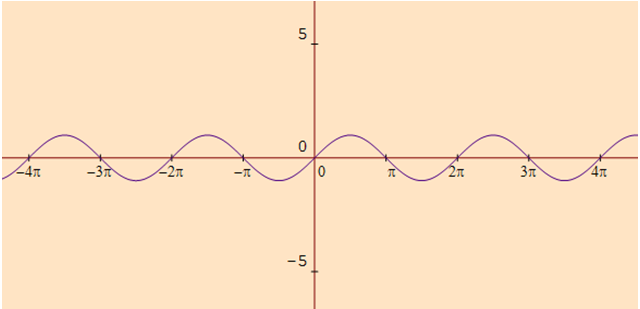
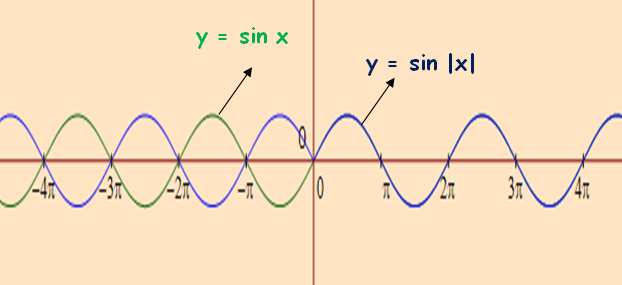
From the curve y = sin x, draw y = sin|x| (Hint: sin(−x) = −sin x.)

Solution :

Graph of y = sin x

(0, 0) (π/2, 1) (π, 0) (3π/2, - 1) and (2π, 0)

To draw the graph of y = sin|x|, let us use the hint

sin(−x) = −sin x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.