TOTAL SURFACE ARE AOF COMBINED SOLID

Problem 1 :

A toy is in the form of right circular cylinder with a hemisphere at the one end and a cone at the other end. The base radius  measures 3.5 cm, height of the cylindrical portion is 10 cm. and conical part measures 12 cm. Find the total surface area of the toy(use π = 3.14)

Solution :

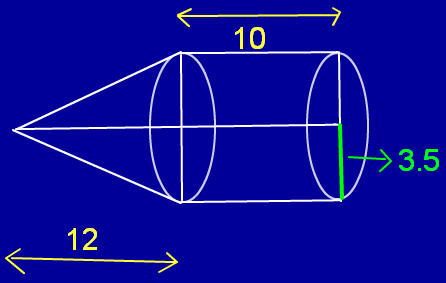
Radius of the hemisphere  =  3.5 cm

Curved Surface area (CSA) of the hemisphere

=  2πr²square units

=  2(3.5)²π

=  (24.5)π cm²

Radius of the Cylinder r = 3.5 cm

Height of the Cylinder h = 10 cm

Curved Surface Area (CSA) of the Cylinder

=  2πrh square units

=  2 π  x 3.5 x 10 

=  70π cm²

Radius of the cone r= 3.5 cm

Height of the cone h = 12 cm

Slant height of the cone l = √(r² + h²)

l  =  √(3.5² + 12²)

l = √(12.25+144)

 l = √(156.25)

l = 12.5 cm

Curved Surface-Area(CSA) of the Cone = πrl square units

=  π(3.5)(12.5)

= (43.75)π cm²

Total Surface-Area of the Toy

=  CSA of the hemisphere +   (CSA of the Cylinder) + (CSA of the Cone)

=  (24.5 π) + (70 π) + (43.75 π)

=  138.25  x 3.14

Hence, total surface area of the Toy = 434.11 cm²

Problem 2 :

Find the total surface area of cylinder whose height is 8 cm and radius is 4 cm.

Solution :

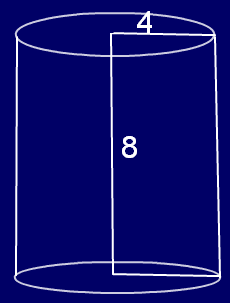
Radius of the Cylinder = 4 cm

Height of the cylinder = 8 cm

Required total surface area of the cylinder = 2πr(h+r)

=  2 π (4) (8+4)

=  2 π (4) (12)

=  96 π

Hence, total surface area of the Cylinder = 96π cm²

Problem 3 :

Find the total surface area of cylinder whose height is 16 cm and radius is 7 cm.

Solution :

Radius of the Cylinder = 7 cm

Height of the cylinder = 16 cm

Required Total surface area of the cylinder  =  2πr(h+r)

=  2 (22/7) (7) (16+7)

= 2 (22) (23)

=  1012 cm²

Hence, Total surface area of the Cylinder = 1012 cm²

Problem 4 :

Find the surface area of the composite solid. 4 m The solid is made up of a square prism and a square pyramid. Use the surface area formulas for a prism and a pyramid, but do not include the areas of the sides that overlap.

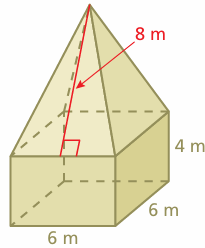
Solution :

Surface area = Area of 4 triangular face + area of 4 rectangular faces + area of one square face at the bottom

= 4 x (1/2) x 6 x 8 + (4 x 6 x 4) + 6 x 6

= (2 x 6 x 8) + (4 x 6 x 4) + 6 x 6

= 96 + 96 + 36

= 228 m²

Problem 5 :

Identify the solids that make up the composite solid. Then fi nd the surface area. Round your answer to the nearest tenth.

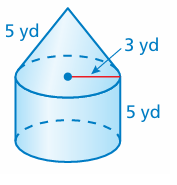
Solution :

Surface area of the shape = surface area of the cylinder + surface area of the cone

= 2πr(h+r) + πrl

Radius = 3 yards, slant height = 5 yards and height of the cylinder = 5 yards

= πr[2(h + r) + l]

= 3.14 x 3[2(5 + 3) + 5]

= 9.42[16 + 5]

= 9.42 (21)

= 197.82 square yards

Problem 6 :

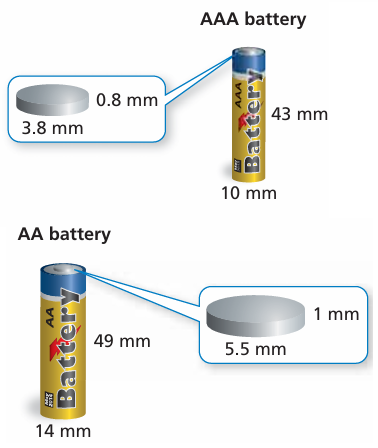
What is the percent increase in the surface area of the AAA battery to the AA battery? Round your answer to the nearest tenth of a percent.

Solution :

Surface area of the AAA battery :

= 2 x 3.14 x 5 x (43 + 5) + 2 x 3.14 x 1.9 x (0.8 + 1.9)

= 31.4 x 48 + 11.932 x 2.7

= 1507.2 + 32.2164

= 1539.4164

Surface area of the AA battery :

= 2 x 3.14 x 7 x (49 + 7) + 2 x 3.14 x 2.25 x (1 + 2.25)

= 43.96 x 56 + 14.13 x 3.25

= 2461.76 + 45.9225

= 2507.6825

Percentage increase in surface area

= [(2507.6825 - 1539.4164) / 1539.4164] x 100%

= (968.2661/1539.4164) x 100%

= 0.628 x 100%

= 62.8%

Approximately surface area is increased by 63%.

Problem 7 :

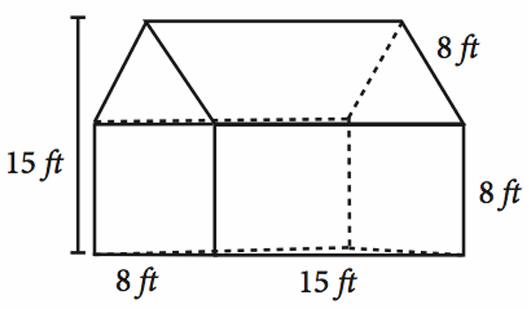
Find the Surface Area of the following. Write your complete solutions, final answers correct to two decimal places. Use pi in your calculator

Solution :

Dimensions of rectangular prism :

length = 15 ft, width = 8 ft and height = 8 ft

Dimension of triangular prism :

base = 8 ft and height = 15 - 8 ==> 7 ft

Surface area of rectangular prism + surface area of triangular prism

= 15 x 8 x 8 + (1/2) x 8 x 7

= 960 + 28

= 988 square feet

Problem 7 :

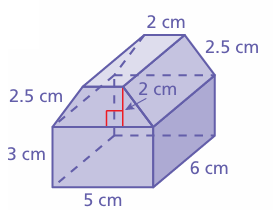
Identify the solids that form the composite solid. Then find the surface area. Round your answer to the nearest tenth.

Solution :

Dimension of rectangular prism :

length = 6 cm, width = 5 cm and height = 3 cm

Surface area of the rectangular prism = l x w + 2(wh + hl)

= 6 x 5 + 2(5 x 3 + 3 x 6)

= 30 + 2(15 + 18)

= 30 + 2(33)

= 30 + 66

= 96 cm²

Dimension of trapezoid prism :

= 2 x area of trapezium + area of rectangles

= 2 x 1/2 x 2 x (5 + 2) + 2(2.5 x 6) + 2 x 6

= 2 x 7 + 2 x 15 + 12

= 14 + 30 + 12

= 56 cm²

Total surface area = 96 + 56

= 152 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.