TIME SPEED AND DISTANCE SHORTCUTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
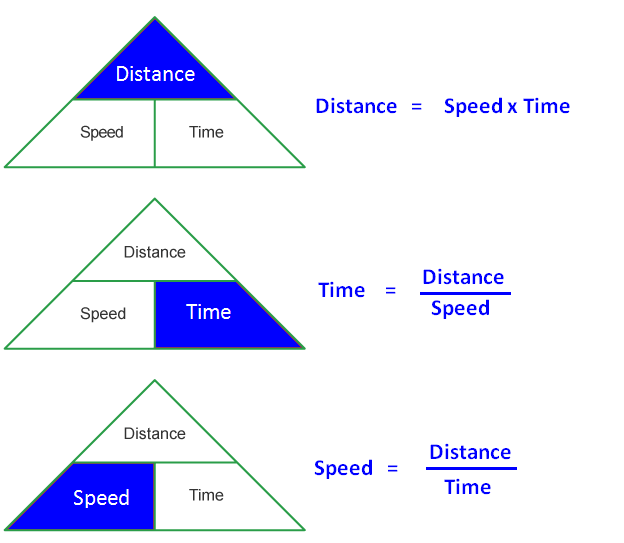
Shortcut 1 :
Let the speed be given in km per hour.
If we want to convert it in to meter per second, then we have to multiply the given speed by 5/18.
Example :
108 km/hr = 108 ⋅ 5/18 meters/sec
108 km/hr = 30 meters/sec
Shortcut 2 :
Let the speed be given in meter per sec.
If we want to convert it in to km per hour, then we have to multiply the given speed by 18/5.
Example :
35 meters/sec = 35 ⋅ 18/5 km/hr
35 meters/sec = 126 km/hr
Shortcut 3 :
Let the speeds of two vehicles be in the ratio a : b.
Then, the ratio of the time taken by the two vehicles to cover the same distance is b : a.
Example :
Let the ratio of speeds of two vehicles be 3 : 4.
Then, the ratio of the time taken by the two vehicles to cover the same distance is 4 : 3.
Shortcut 4 :
Let the speeds of two vehicles be in the ratio a : b.
Then, the ratio of distances covered by the two vehicles in the same amount of time is also a : b.
Example :
Let the ratio of speeds of two vehicles be 3 : 4. Each vehicle is given one hour time. Then, the distance covered by the two vehicles will be in the ratio 3 : 4.
Shortcut 5 :
Let A be twice as fast as B.
Then, the ratio of distances covered by A and B in the same amount of time will be 2 : 1.
Example :
Let A be twice as fast as B and each given 1 hour time. If A covers 40 miles of distance, then B will cover 20 miles of distance.
Shortcut 6 :
Let the speed of a vehicle be increased or decreased in the ratio a : b.
Then the new speed is
= b of the original speed/a
More clearly, new speed is
= (b ⋅ original speed)/ a
Example :
Michael travels at a speed of 63 miles per hour. If he reduces his speed in the ratio 9 : 8, find his new speed.
new speed = (8 ⋅ 63)/9
= 56 miles per hour
Shortcut 7 :
A vehicle covers a particular distance at a speed “a” miles per hour and comes back to its original position at a speed of “b” miles per hour.
Then the average speed for the total distance covered is
= 2ab/(a + b) miles hour
Important condition :
The distance covered in 'a' miles per hour and the distance covered in 'b' miles per hour must be same.
Example :
Kevin covers 300 miles at the speed 45 mph and travels another 300 miles at the speed of 55 mph. Find the average speed for the whole journey.
Average speed for the whole journey is
= (2 ⋅ 45 ⋅ 55)/(45 + 55)
= 4950/90
= 55 miles per hour

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
