THIRD ANGLE THEOREM
If two angles of one triangle are congruent to two angles of another triangle, then the third pair of angles must also be congruent.
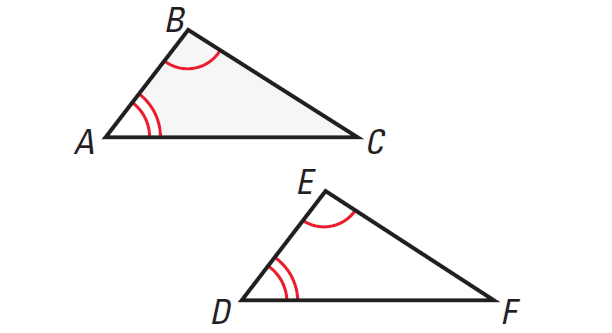
In the diagram given below, if ∠A ≅ ∠D and∠B ≅ ∠E, then ∠C ≅ ∠F.
Example 1 :
In the diagram given below, ∠L ≅ ∠P and ∠M ≅ ∠Q, find m∠N and m∠R. Check whether ∠N ≅ ∠R and justify your answer.
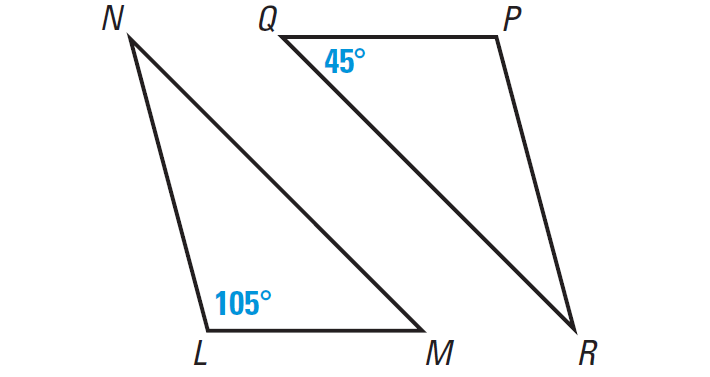
Solution :
Given : ∠L ≅ ∠P and ∠M ≅ ∠Q
|
From the figure above, we have m∠L = 105° Because ∠L ≅ ∠P, we have m∠P = 105° |
From the figure above, we have m∠Q = 45° Because ∠Q ≅ ∠M, we have m∠M = 45° |
ΔLMN :
By the Triangle Sum theorem, we have
m∠L + m∠M + m∠N = 180°
Substitute 105° for m∠L and 45° for m∠M.
105° + 45° + m∠N = 180°
Simplify.
150° + m∠N = 180°
Subtract 150° from both sides.
m∠N = 30°
ΔPQR :
By the Triangle Sum theorem, we have
m∠P + m∠Q + m∠R = 180°
Substitute 105° for m∠P and 45° for m∠Q.
105° + 45° + m∠R = 180°
Simplify.
150° + m∠R = 180°
Subtract 150° from both sides.
m∠R = 30°
Because m∠N = 30° and m∠R = 30°, we have
m∠N = m∠R -----> ∠N ≅ ∠R
Justification :
By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, ∠N ≅ ∠R
Example 2 :
In the diagram given below, ∠B ≅ ∠U and ∠C ≅ ∠V, find m∠A and using the Third Angles Theorem to find m∠T.
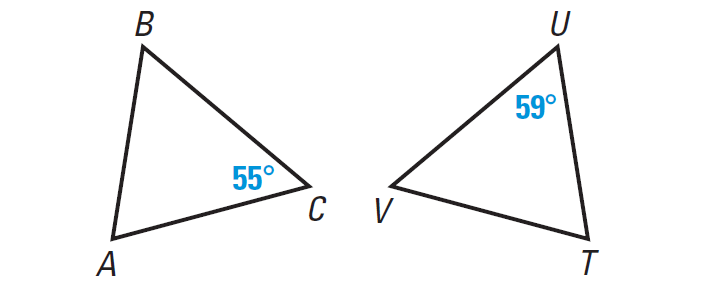
Solution :
Given : ∠B ≅ ∠U and ∠C ≅ ∠V.
From the figure, we have m∠U = 59°.
Because ∠B ≅ ∠U, we have m∠B = 59°.
In ΔABC, by the Triangle Sum theorem, we have
m∠A + m∠B + m∠C = 180°
Substitute 59° for m∠B and 55° for m∠C.
m∠A + 59° + 55° = 180°
Simplify.
m∠A + 114° = 180°
Subtract 114° from both sides.
m∠A = 66°
By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠T ≅ ∠A
m∠T = ∠A
m∠T = 66°
Example 3 :
Find the value of x in the diagram given below.
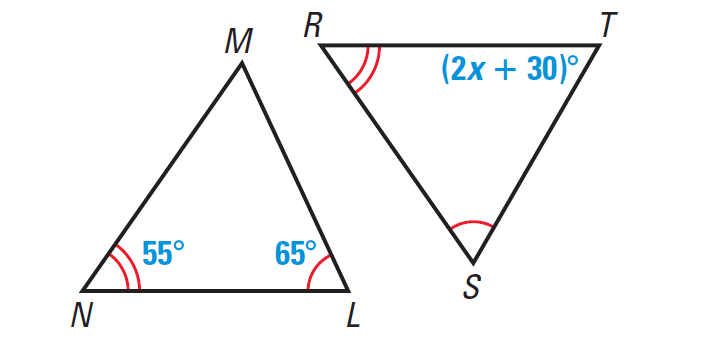
Solution :
In the diagram above, ∠N ≅ ∠R and ∠L ≅ ∠S. From the Third angles theorem, we know that ∠M ≅ ∠T. So, m∠M = m∠T.
From the triangle sum theorem, we have
m∠L + m∠M + m∠N = 180°
65° + 55° + m∠M = 180°
Simplify
120° + m∠M = 180°
Subtract 120° from both sides.
m∠M = 60°
By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠M ≅ ∠T ----> m∠M = m∠T
Substitute 60° for m∠M and (2x + 30)° for m∠M.
60° = (2x + 30)°
60 = 2x + 30
Subtract 30 from both sides.
30 = 2x
Divide both sides by 2.
15 = x
Example 4 :
Decide whether the triangles are congruent. Justify your reasoning.
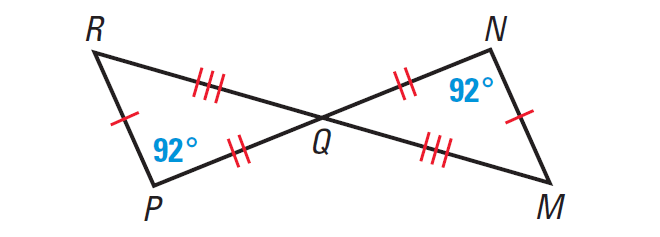
Solution :
From the diagram, we are given that all three pairs of corresponding sides are congruent.
RP ≅ MN, PQ ≅ NQ and QR ≅ QM
Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.
By the Vertical Angles Theorem, we know that
∠PQR ≅ ∠MQN
In ΔPQR and ΔMQN, ∠P ≅ ∠N and ∠PQR ≅ ∠MQN.
By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠R ≅ ∠M
So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent.
By the definition of congruent angles,
ΔPQR ≅ ΔNQM

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
