THIRD ANGLE THEOREM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If two angles of one triangle are congruent to two angles of another triangle, then the third pair of angles must also be congruent.
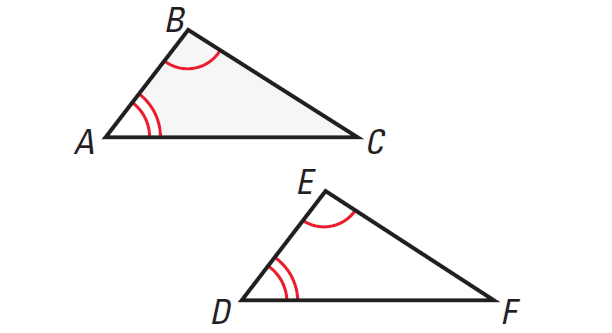
In the diagram given below, if ∠A ≅ ∠D and∠B ≅ ∠E, then ∠C ≅ ∠F.
Example 1 :
In the diagram given below, ∠L ≅ ∠P and ∠M ≅ ∠Q, find m∠N and m∠R. Check whether ∠N ≅ ∠R and justify your answer.
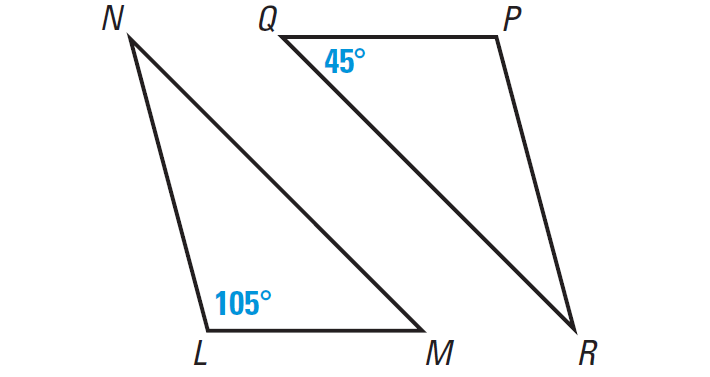
Solution :
Given : ∠L ≅ ∠P and ∠M ≅ ∠Q
|
From the figure above, we have m∠L = 105° Because ∠L ≅ ∠P, we have m∠P = 105° |
From the figure above, we have m∠Q = 45° Because ∠Q ≅ ∠M, we have m∠M = 45° |
ΔLMN :
By the Triangle Sum theorem, we have
m∠L + m∠M + m∠N = 180°
Substitute 105° for m∠L and 45° for m∠M.
105° + 45° + m∠N = 180°
Simplify.
150° + m∠N = 180°
Subtract 150° from both sides.
m∠N = 30°
ΔPQR :
By the Triangle Sum theorem, we have
m∠P + m∠Q + m∠R = 180°
Substitute 105° for m∠P and 45° for m∠Q.
105° + 45° + m∠R = 180°
Simplify.
150° + m∠R = 180°
Subtract 150° from both sides.
m∠R = 30°
Because m∠N = 30° and m∠R = 30°, we have
m∠N = m∠R -----> ∠N ≅ ∠R
Justification :
By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, ∠N ≅ ∠R
Example 2 :
In the diagram given below, ∠B ≅ ∠U and ∠C ≅ ∠V, find m∠A and using the Third Angles Theorem to find m∠T.
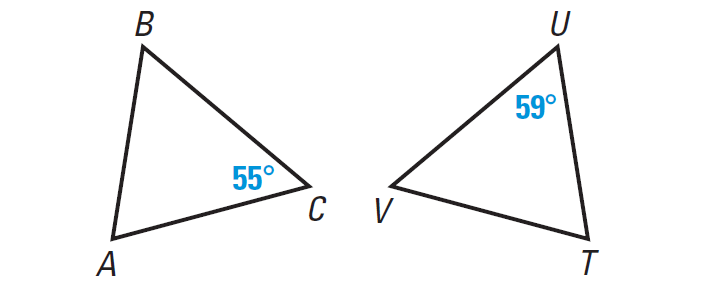
Solution :
Given : ∠B ≅ ∠U and ∠C ≅ ∠V.
From the figure, we have m∠U = 59°.
Because ∠B ≅ ∠U, we have m∠B = 59°.
In ΔABC, by the Triangle Sum theorem, we have
m∠A + m∠B + m∠C = 180°
Substitute 59° for m∠B and 55° for m∠C.
m∠A + 59° + 55° = 180°
Simplify.
m∠A + 114° = 180°
Subtract 114° from both sides.
m∠A = 66°
By the Third Angles Theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠T ≅ ∠A
m∠T = ∠A
m∠T = 66°
Example 3 :
Find the value of x in the diagram given below.
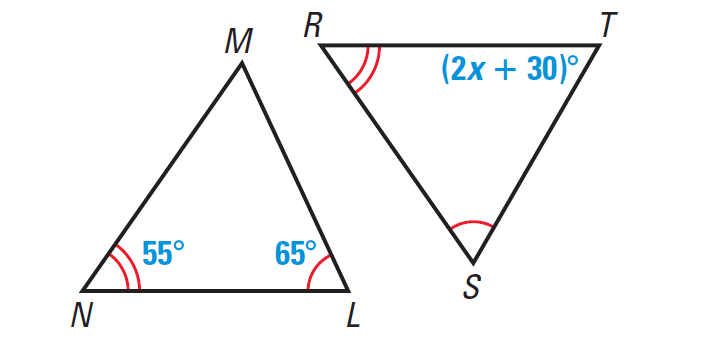
Solution :
In the diagram above, ∠N ≅ ∠R and ∠L ≅ ∠S. From the Third angles theorem, we know that ∠M ≅ ∠T. So, m∠M = m∠T.
From the triangle sum theorem, we have
m∠L + m∠M + m∠N = 180°
65° + 55° + m∠M = 180°
Simplify
120° + m∠M = 180°
Subtract 120° from both sides.
m∠M = 60°
By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠M ≅ ∠T ----> m∠M = m∠T
Substitute 60° for m∠M and (2x + 30)° for m∠M.
60° = (2x + 30)°
60 = 2x + 30
Subtract 30 from both sides.
30 = 2x
Divide both sides by 2.
15 = x
Example 4 :
Decide whether the triangles are congruent. Justify your reasoning.
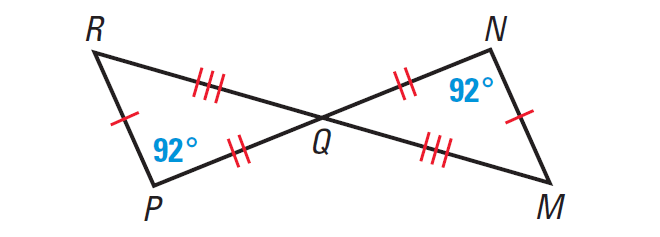
Solution :
From the diagram, we are given that all three pairs of corresponding sides are congruent.
RP ≅ MN, PQ ≅ NQ and QR ≅ QM
Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.
By the Vertical Angles Theorem, we know that
∠PQR ≅ ∠MQN
In ΔPQR and ΔMQN, ∠P ≅ ∠N and ∠PQR ≅ ∠MQN.
By the theorem, if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
So, we have
∠R ≅ ∠M
So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent.
By the definition of congruent angles,
ΔPQR ≅ ΔNQM
Example 5 :
The triangle are similar, find the value of x.
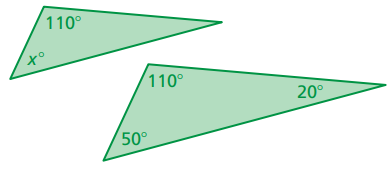
Solution :
Since the above triangles are similar, corresponding angles will be equal and measures of corresponding sides will be in the same ratio.
x = 50
Example 6 :
In the diagram below triangles ABC and QLP are similar.
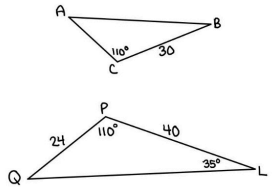
a) Which side can you find in triangle ABC? Find that side.
b) Find the measure of ∠Q in the triangle.
c) Use the angles in triangle QLP to find all the missing angles in triangle ABC.
d) Extra: Write a ratio that would be equivalent to PL/PQ.
Solution :
a) Since the triangles are similar,
AB and QL are corresponding sides.
- <B and <L are corresponding angles.
- <A and <Q are corresponding angles.
- <C and <P are corresponding angles.
a)
AB/QL = AC/QP = BC/PL
AC/24 = 30/40
AC/24 = 3/4
AC = (3/4) x 24
AC = 18
b) In triangle QLP,
<P + <Q + <L = 180
110 + <Q + 35 = 180
<Q + 145 = 180
<Q = 180 - 145
<Q = 35
c) In triangle ABC, <B = 35 and <A = 35
d) PL/PQ = 40/24
= 5/3
Example 6 :
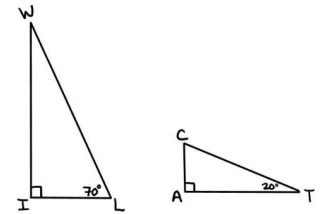
a) Find the missing angle in each triangle. How does this show that the triangles are similar?
b) If WI = 9.4 and WL = 10. Find the side IL using the Pythagorean Theorem (to one decimal)
c) If the scale factor from triangle WIL to triangle ATC is ½, find all the missing sides of triangle TAC.
Solution :
In triangle WIL,
<W + <I + <L = 180
<W + 90 + 70 = 180
<W + 160 = 180
<W = 180 - 160
<W = 20
Since the triangles are equiangular, they are similar.
b)
WL2 = WI2 + IL2
102 = 9.42 + IL2
100 - 88.36 = IL2
IL2 = 11.64
IL = 3.4
c) WL/TC = IL/AT = WI/AC
10 / TC = 3.4/AT = 9.4/AC = 1/2
|
10/TC = 1/2 TC = 20 |
3.4/AT = 1/2 AT = 3.4(2) = 6.8 |
9.4/AC = 1/2 AC = 9.4(2) = 18.8 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
