PYTHAGOREAN THEOREM

In this section, we are going to study one of the most famous theorems in mathematics — the Pythagorean Theorem. The relationship it describes has been known for thousands of years.

Theorem :

In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two legs.

It has been illustrated in the diagram shown below. 

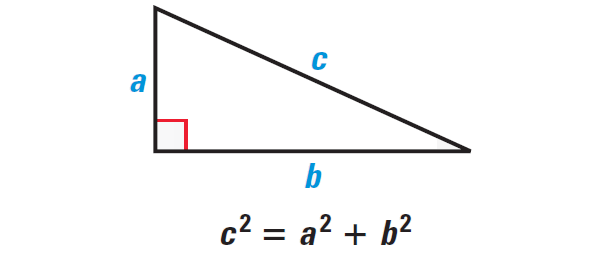
Proving the Pythagorean Theorem

There are many different proofs of the Pythagorean Theorem. One is shown below.

Given : In ΔABC, ∠BCA is a right angle. 

Prove : a² + b² = c²

Plan for Proof : 

Draw altitude CD to the hypotenuse. Then apply Geometric Mean Theorem, which states that when the altitude is drawn to the hypotenuse of a right triangle, each leg of the right triangle is the geometric mean of the hypotenuse and the segment of the hypotenuse that is adjacent to that leg.

Using Pythagorean Theorem

A Pythagorean triple is a set of three positive integers a, b, and c that satisfy the equation

c²  =  a² + b²

For example, the integers 3, 4 and 5 form a Pythagorean triple. 

Because, 

5²  =  3² + 4²

Finding the Length of a Hypotenuse 

Example 1 :

Find the length of the hypotenuse of the right triangle shown below. Tell whether the side lengths form a Pythagorean triple.

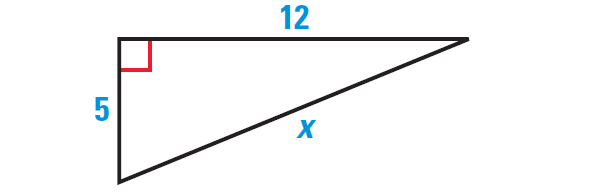
Solution :

By Pythagorean Theorem, we have

(Hypotenuse)²  =  (leg)² + (leg)²

Substitute.

x²  =  5² + 12²

Simplify.

x²  =  25 + 144

x²  =  169

Take square root on each side.

√x²  =  √169

x  =  13

So, the length of the hypotenuse is 13 units. 

Because 13²  =  12² + 5², they form a Pythagorean triple. 

Finding the Length of a Leg

Example 2 :

Find the length of the leg of the right triangle shown below. 

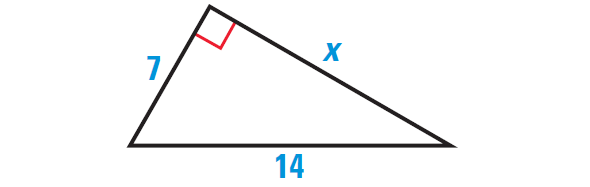
Solution :

By Pythagorean Theorem, we have

(Hypotenuse)²  =  (leg)² + (leg)²

Substitute.

14²  =  7² + x²

Simplify.

196  =  49 + x²

Subtract 49 from each side. 

147  =  x²

Take square root on each side.

√147  =  √x²

√147  =  x

Use product property.

√49 ⋅ √3  =  x

Simplify the radical. 

7√3  =  x 

Hence, the required side length is 7√3 units. 

Finding the Area of a Triangle

Example 3 :

Find the area of the triangle to the nearest tenth of a meter.

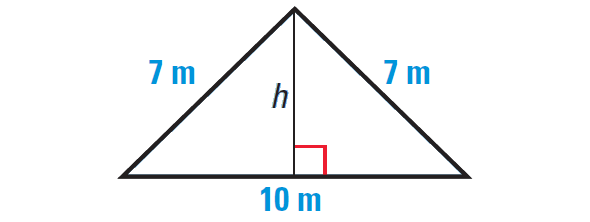
Solution :

We are given that the base of the triangle is 10 meters, but we do not know the height h.

Because the triangle is isosceles, it can be divided into two congruent right triangles with the given dimensions. Use the Pythagorean Theorem to find the value of h.

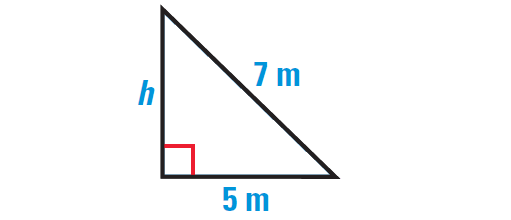
By Pythagorean Theorem, we have

7²  =  5² + h²

Simplify.

49  =  25 + h²

Subtract 25 from each side.

24  =  h²

Take square root on each side.

√24  =  √h²

√24  =  h

Now find the area of the original triangle. 

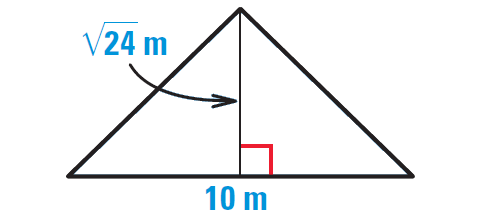
Area  =  1/2 ⋅ b ⋅ h

Substitute.

Area  =  1/2 ⋅ 10 ⋅ √24

Use calculator to approximate. 

Area  =  1/2 ⋅ 10 ⋅ √24

Area  ≈  24.5 m²

Hence, the area of the triangle is about 24.5 m².

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.