THE MIDPOINT AND DISTANCE FORMULAS
The midpoint of a line segment is the point that divides the segment into two congruent segments. Congruent segments are segments that have the same length.
You can find the midpoint of a segment by using the coordinates of its endpoints. Calculate the average of the x-coordinates and the average of the y-coordinates of the endpoints.
Midpoint Formula
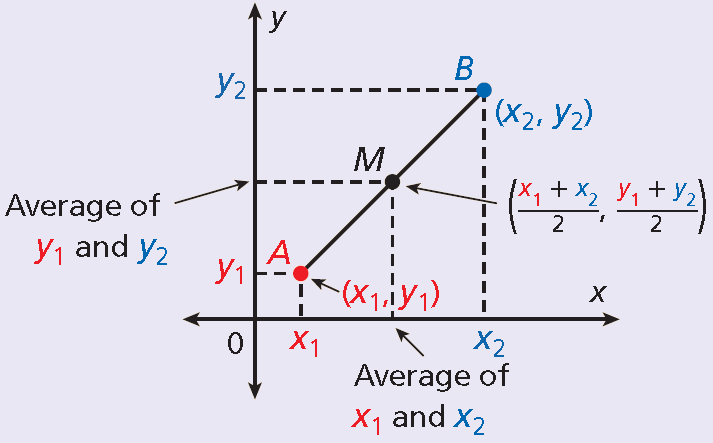
Let A(x1, y1) and B(x2, y2).
The midpoint M of the line segment AB is
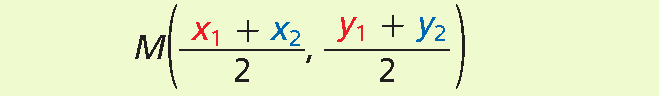
Finding the Coordinates of a Midpoint
Example 1 :
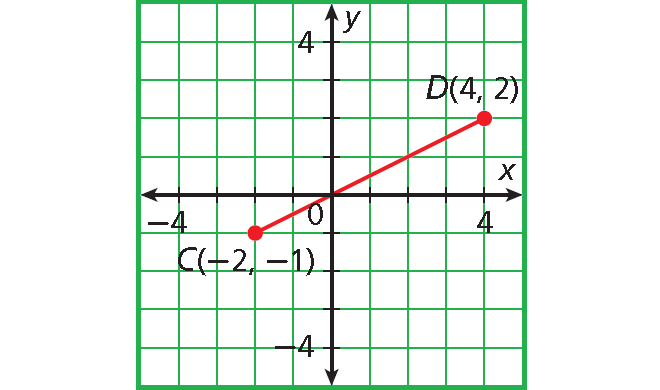
Find the coordinates of the midpoint of the line segment CD with endpoints C(-2, -1) and D (4, 2).
Solution :
Write the formula.
= M[(x1 + x2)/2, (y1 + y2)/2]
Substitute (-2, -1) for (x1, y1) and (4, 2) for (x2, y2).
= M[(-2 + 4)/2, (-1 + 2)/2]
= M(2/2, 1/2)
= M(1, 1/2)
Finding the Coordinates of an Endpoint
Example 2 :
M is the midpoint of the line segment AB. A has coordinates (2, 2), and M has coordinates (4, -3). Find the coordinates of B.
Solution :
Step 1 :
Let the coordinates of B equal (x, y).
Step 2 :
Use the Midpoint Formula.
(4, -3) = [(2 + x)/2, (2 + y)/2]
Step 2 :
|
Find the x-coordinate. 4 = (2 + x)/2 8 = 2 + x 6 = x |
Find the y-coordinate. -3 = (2 + y)/2 -6 = 2 + y -8 = y |
The coordinates of B are (6, –8).
Check :
Graph points A and B and midpoint M.
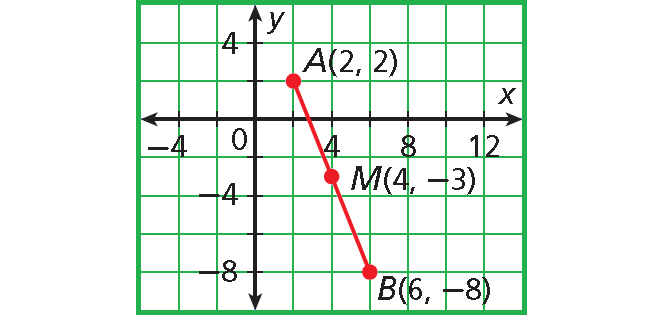
Point M appears to be the midpoint of the line segment AB.
You can also use coordinates to find the distance between two points or the length of a line segment.
To find the length of segment PQ, draw a horizontal segment from P and a vertical segment from Q to form a right triangle as shown below.
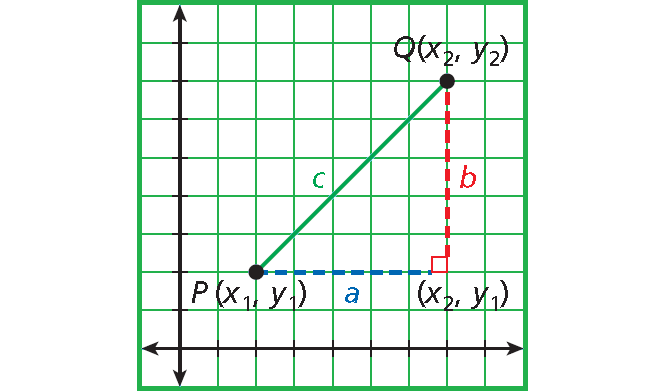
Pythagorean Theorem :
c2 = a2 + b2
Solve for c. Use the positive square root to represent distance.
c = √(a2 + b2)
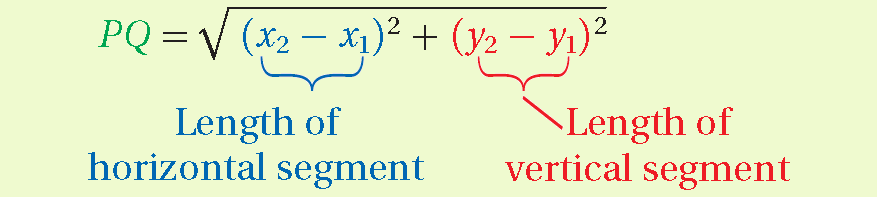
This equation represents the Distance Formula.
Distance Formula
In a coordinate plane, formula to find the distance between two points (x1, y1) and (x2, y2) is
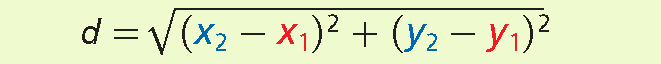
Finding Distance in the Coordinate Plane
Example 3 :
Use the Distance Formula to find the distance, to the nearest hundredth, from A(-2, 3) to B(2, -2).
Solution :
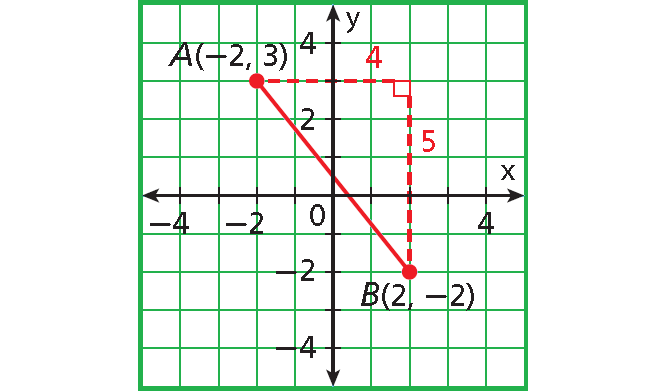
Distance Formula :
d = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (-2, 3) for (x1, y1) and (2, -2) for (x2, y2).
d = √[(2 + 2)2 + (-2 - 3)2]
Simplify.
d = √[42 + (-5)2]
d = √[16 + 25]
d = √41
d ≈ 6.40
The distance between from A(-2, 3) to B(2, -2) is about 6.40 units.
Geography Application
Example 4 :
Each unit on the map of Lake Okeechobee represents 1 mile. Kemka and her father plan to travel from point A near the town of Okeechobee to point B at Pahokee. To the nearest tenth of a mile, how far do Kemka and her father plan to travel?
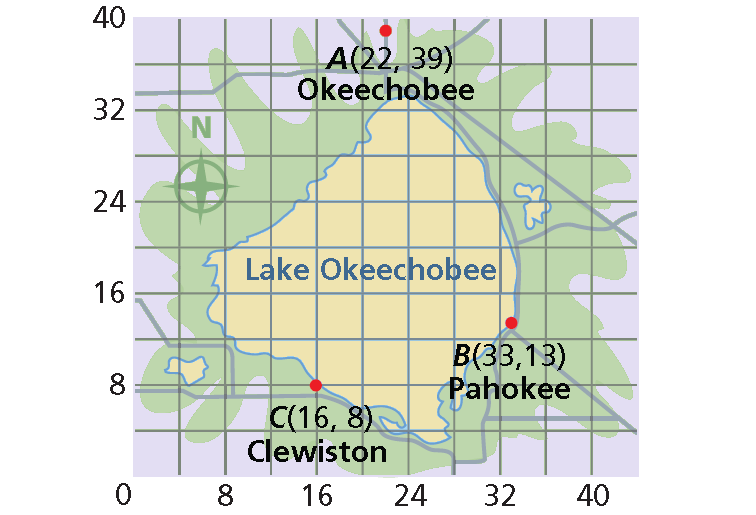
Solution :
Distance Formula :
d = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (33, 13) for (x1, y1) and (22, 39) for (x2, y2).
d = √[(33 - 22)2 + (13 - 39)2]
Simplify.
d = √[112 + (-26)2]
d = √[121 + 676]
d = √797
d ≈ 28.2
Kemka and her father plan to travel about 28.2 miles.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and Venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
©All rights reserved. onlinemath4all.com
Recent Articles
-
Linear vs Exponential Growth
May 23, 22 01:59 AM
Linear vs Exponential Growth - Concept - Examples
-
Exponential vs Linear Growth Worksheet
May 23, 22 01:42 AM
Exponential vs Linear Growth Worksheet
-
SAT Math Questions on Exponential vs Linear Growth
May 23, 22 01:34 AM
SAT Math Questions on Exponential vs Linear Growth