THE CONVERSE OF THE PYTHAGOREAN THEOREM WORKSHEET
Problem 1 :
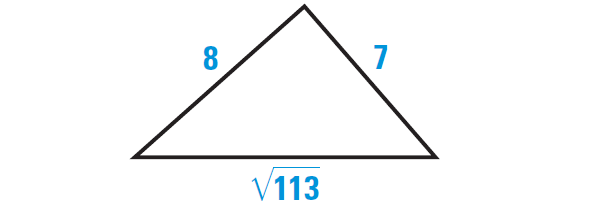
The triangle shown below appears to be a right triangle. Say whether it is right a triangle.
Problem 2 :
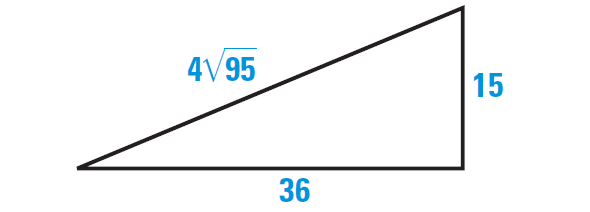
The triangle shown below appears to be a right triangle. Say whether it is right a triangle.
Problem 3 :
Decide whether the set of numbers given below can represent the side lengths of a triangle. If they can, classify the triangle as right, acute, or obtuse.
38, 77, 86
Problem 4 :
Decide whether the set of numbers given below can represent the side lengths of a triangle. If they can, classify the triangle as right, acute, or obtuse.
10, 36, 37
Problem 5 :
Decide whether the set of numbers given below can represent the side lengths of a triangle. If they can, classify the triangle as right, acute, or obtuse.
30, 40, 50
Problem 6 :
We use four stakes and string to mark the foundation of a house. We want to make sure the foundation is rectangular.
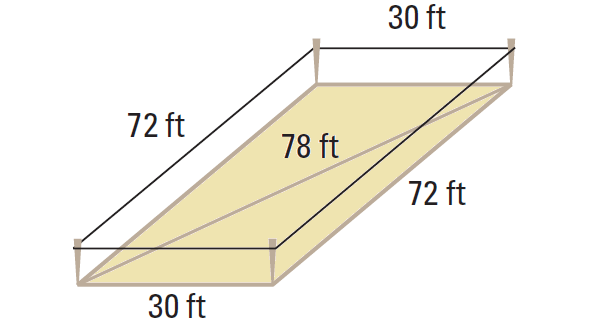
(i) John measures the four sides to be 30 feet, 30 feet, 72 feet, and 72 feet. He says these measurements prove the foundation is rectangular. Is he correct ?
(ii) David measures one of the diagonals to be 78 feet. Explain how David can use this measurement to tell whether the foundation will be rectangular.

Answers
1. Answer :

Let c represent the length of the longest side of the triangle. Check to see whether the side lengths satisfy the equation
c2 = a2 + b2
Substitute.
(√113)2 = 72 + 82 ?
113 = 49 + 64 ?
113 = 113
Because the lengths of the sides of the triangle satisfy the equation c2 = a2 + b2, the triangle shown above is a right triangle.
2. Answer :

Let c represent the length of the longest side of the triangle. Check to see whether the side lengths satisfy the equation
c2 = a2 + b2
Substitute.
(4√95)2 = 152 + 362 ?
42 ⋅ (√95)2 = 152 + 362 ?
16 ⋅ 95 = 225 + 1296 ?
1520 ≠ 1521
Because the lengths of the sides of the triangle do not satisfy the equation c2 = a2 + b2, the triangle shown above is not a right triangle.
3. Answer :
38, 77, 86
By Triangle Inequality Theorem, the above set of numbers can represent the side lengths of a triangle.
Compare the square of the length of the longest side with the sum of the squares of the lengths of the two shorter sides.
Compare c2 with a2 + b2.
c2 ? a2 + b2
Substitute.
862 ? 382 + 772
7396 ? 1444 + 5929
7396 > 1444 + 5929
c2 > a2 + b2
Because c2 is greater than a2 + b2, the triangle is obtuse.
4. Answer :
10, 36, 37
By Triangle Inequality Theorem, the above set of numbers can represent the side lengths of a triangle.
Compare the square of the length of the longest side with the sum of the squares of the lengths of the two shorter sides.
Compare c2 with a2 + b2.
c2 ? a2 + b2
Substitute.
372 ? 102 + 362
1369 ? 100 + 1296
1369 < 1396
c2 < a2 + b2
Because c2 is less than a2 + b2, the triangle is acute.
5. Answer :
30, 40, 50
By Triangle Inequality Theorem, the above set of numbers can represent the side lengths of a triangle.
Compare the square of the length of the longest side with the sum of the squares of the lengths of the two shorter sides.
Compare c2 with a2 + b2.
c2 ? a2 + b2
Substitute.
502 ? 302 + 402
2500 ? 900 + 1600
2500 = 2500
c2 = a2 + b2
Because c2 is equal to a2 + b2, the triangle is right.
6. Answer :

(i) John measures the four sides to be 30 feet, 30 feet, 72 feet, and 72 feet. He says these measurements prove the foundation is rectangular. Is he correct ?
(ii) David measures one of the diagonals to be 78 feet. Explain how David can use this measurement to tell whether the foundation will be rectangular.
Part (i) :
John is not correct. The foundation could be a nonrectangular parallelogram, as shown below.
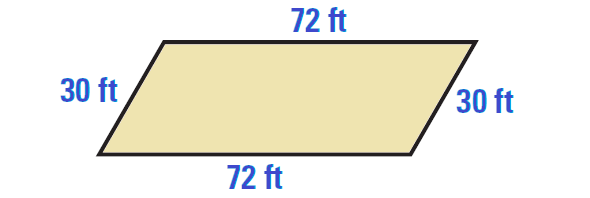
Part (ii) :
The diagonal divides the foundation into two triangles. Compare the square of the length of the longest side with the sum of the squares of the shorter sides of one of these triangles.
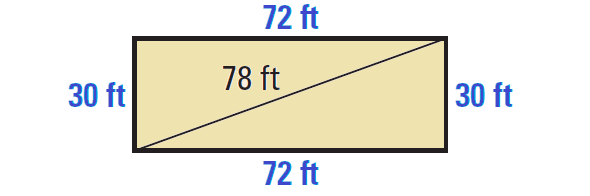
Because 302 + 722 = 782, David can conclude that both the triangles are right triangles.
The foundation is a parallelogram with two right angles, which implies that it is rectangular.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 30)
Oct 17, 25 07:27 PM
10 Hard SAT Math Questions (Part - 30) -
10 Hard SAT Math Questions (Part - 29)
Oct 16, 25 06:04 AM
10 Hard SAT Math Questions (Part - 29) -
10 Hard SAT Math Questions (Part - 28)
Oct 14, 25 10:57 AM
10 Hard SAT Math Questions (Part - 28)