TANGENTS TO CIRCLES WORKSHEET

Problem 1 :

Tell which line or segment is best described as a tangent in the diagram shown below. 

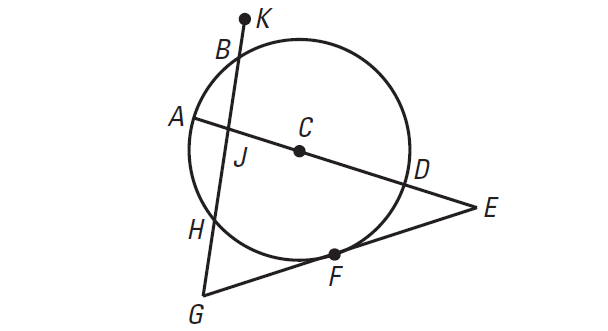
Problem 2 :

In the diagram shown below, tell whether the common tangents are internal or external. 

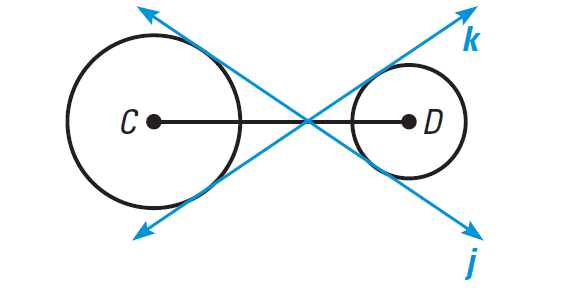
Problem 3 :

In the diagram shown below, tell whether the common tangents are internal or external.  

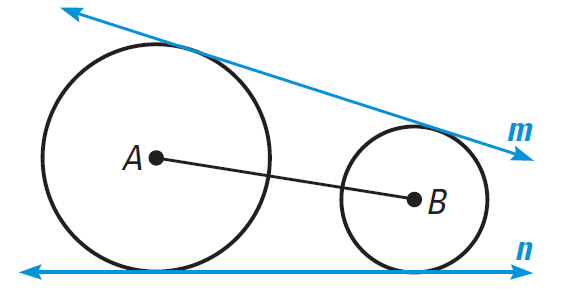
Problem 4 :

In the diagram shown below, describe all common tangent and identify the point of tangency. 

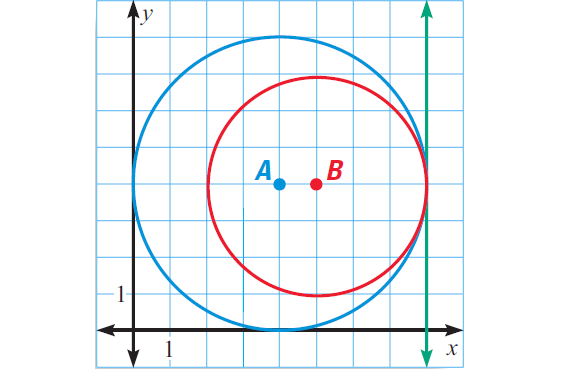
Problem 5 :

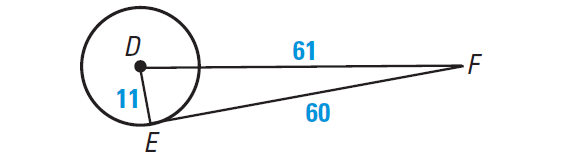
In the diagram shown below, say whether EF is tangent to the circle with center at D.

Problem 6 :

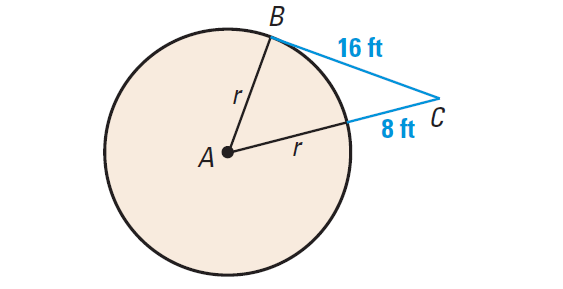
In the diagram shown below, I am standing at C, 8 feet from a grain silo. The distance from me to a point of tangency is 16 feet. What is the radius of the silo ? 

Problem 7 :

In the diagram shown below, 

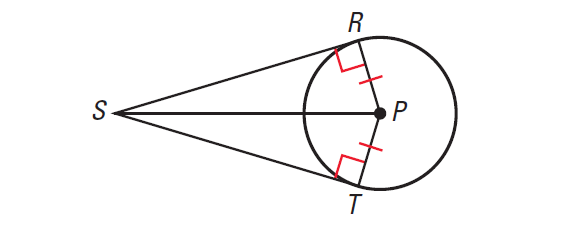
SR is tangent at R to the circle with center P

ST is tangent at T to the circle with center P

Prove : SR  ≅  ST

Problem 8 :

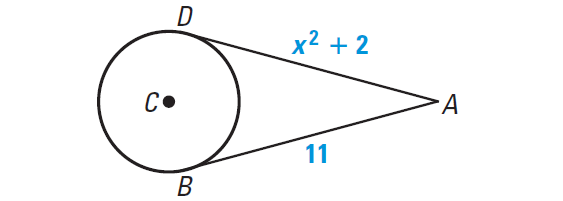
In the diagram shown below, 

AB is tangent at B to the circle with center at C

AD is tangent at D to the circle with center at C

Find the value of x.

Answers

Problem 1 :

Tell which line or segment is best described as a tangent in the diagram shown below.   

Answer :

EG is a tangent, because it intersects the circle in one point. 

Problem 2 :

In the diagram shown below, tell whether the common tangents are internal or external.  

Answer :

The lines j and k intersect CD, they are common internal tangents. 

Problem 3 :

In the diagram shown below, tell whether the common tangents are internal or external.  

Answer :

The lines m and n do not intersect AB, so they are common external tangents. 

Problem 4 : 

In the diagram shown below, describe all common tangent and identify the point of tangency. 

Answer :

The vertical line x  =  8 is the only common tangent of the two circles. 

The point of tangency is (8, 4). 

Note : 

The point at which a tangent line intersects the circle to which it is tangent is the point of tangency. 

Problem 5 : 

In the diagram shown below, say whether EF is tangent to the circle with center at D.  

Answer :

We can use the Converse of the Pythagorean Theorem to say whether EF is tangent to circle with center at D.  

Because 112 + 602  =  612, ΔDEF is a right triangle and DE is perpendicular to EF.

So by Theorem 2, EF is tangent to the circle with center at D.  

Problem 6 :

In the diagram shown below, I am standing at C, 8 feet from a grain silo. The distance from me to a point of tangency is 16 feet. What is the radius of the silo ?    

Answer :

By the Theorem 1,  tangent BC is perpendicular to radius AB at B. So ΔABC is a right triangle. So we can use the Pythagorean theorem.  

Pythagorean Theorem :

(r + 8)²  =  r² + 16²

Square of binomial :

r² + 16r + 64  =  r² + 256

Subtract r² from each side : 

16r + 64  =  256

Subtract 64 from each side : 

16r  =  192

Divide each side by 16. 

r  =  12

Hence, the radius of the silo is 12 feet. 

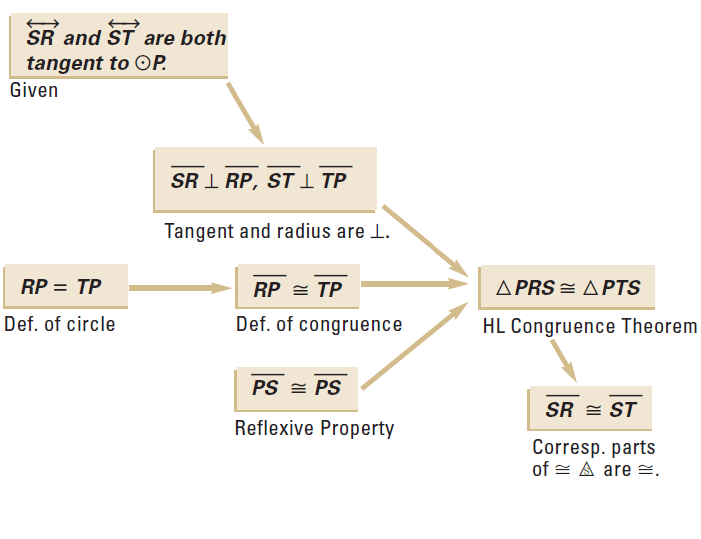
Problem 7 : 

In the diagram shown below, 

SR is tangent at R to the circle with center P

ST is tangent at T to the circle with center P

Prove : SR  ≅  ST

Answer :

Problem 8 :

In the diagram shown below, 

AB is tangent at B to the circle with center at C

AD is tangent at D to the circle with center at C

Find the value of x. 

Answer :

By the Theorem 3, two tangent segments from the same point are congruent.

AB  =  AD

Substitute : 

x² + 2  =  11

Subtract 2 from each side. 

x²  =  9

Take square root on each side. 

x  =  ± 3

Hence, the value of x is 3 or -3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.