FIND EQUATION OF TANGENT TO THE CURVE WHICH IS PARALLEL TO THE LINE
Example 1 :
Find the equations of those tangents to the circle
x2 + y2 = 52
which are parallel to the straight line 2x + 3y = 6.
Solution :
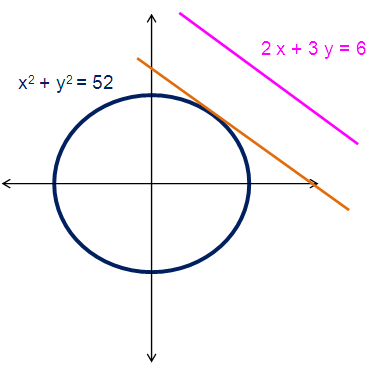
If two lines are parallel, then slopes of those lines will be equal.
Here,
slope of tangent = slope of the given line
Slope of the given line 2x + 3y = 6
m = -coefficient of x/coefficient of y
m = -2/3 ----(1)
Slope of the tangent line drawn to the circle
2x + 2y(dy/dx) = 0
dy/dx = -x/y ----(2)
(1) = (2)
-2/3 = -x/y
2y = 3x
y = 3x/2
Substituting the value of y in the equation of curve.
x2 + y2 = 52
x2 + (3x/2)2 = 52
x2 + (9x2/4) = 52
13x2/4 = 52
x2 = 16
x = ± 4
|
If x = 4, then y = 6 |
If x = -4, then y = -6 |
So, the point of contact are (4, 6) (-4, -6).
Equation of the tangent passing through the point (4, 6) and m = -2/3.
y - y1 = m(x - x1)
y - 6 = (-2/3)(x - 4)
3(y - 6) = -2(x - 4)
3y - 18 = -2x + 8
2x + 3y - 8 - 18 = 0
2x + 3y - 26 = 0
Equation of the tangent passing through the point (-4, -6) and m = -2/3.
y + 6 = (-2/3)(x + 4)
3(y + 6) = -2(x + 4)
3y + 18 = -2x - 8
2x + 3y + 26 = 0
Example 1 :
Find the equations of normal to
y = x3 - 3x
that is parallel to 2x + 18y - 9 = 0.
Solution :
Slope of tangent drawn to the circle.
dy/dx = 3x2 - 3(1)
= 3x2 - 3
Slope of the normal line to the curve
= -1/(3x2 - 3) ----(2)
Slope of the line parallel to the normal line to the curve
m = -coefficient of x/coefficient of y
m = -2/18
m = -1/9 ----(1)
(1) = (2)
-1/9 = -1/(3x2 - 3)
3x2 - 3 = 9
x2 = 12/3
x2 = 4
x = √4
x = ±2
|
x = 2 y = 23 - 3(2) y = 2 |
x = -2 y = (-2)3 - 3(-2) y = -2 |
points of contact are (2, 2) (-2, -2).
Equation of the normal passing through the point
(2, 2) and m = -1/9
y - 2 = (-1/9)(x - 2)
9(y - 2) = -1(x - 2)
9y - 18 = -x + 2
x + 9y - 20 = 0
Equation of the normal passing through the point
(-2, -2) and m = -1/9
y + 2 = (-1/9)(x + 2)
9(y + 2) = -1(x + 2)
9y + 18 = -x - 2
x + 9y + 20 = 0
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 10:07 AM
Writing Quadratic Functions in Standard Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
