SYSTEMS OF MEASURING ANGLES

There are three different systems for measuring angles.

(i) Sexagesimal System or British System :

The Sexagesimal system is the most prevalent system of measurement where a right angle is divided into 90 equal parts called Degrees. Each degree is divided into 60 equal parts called Minutes, and each minute into 60 equal parts called Seconds.

The symbols 1°, 1' and 1" are used to denote a degree, a minute and a second respectively.

In short,

1 right angle  =  90° (or 90 degrees)

1° (or 1 degree)  =  60' (or 60 minutes)

1' (or 1 minute)  =  60" (or 60 seconds)

(ii) Centesimal System or French System :

In the Centesimal system , the right angle is divided into 100 equal parts, called Grades ; each grade is subdivided into 100 Minutes, and each minute is subdivided into 100 Seconds.

The symbol 1^g is used to denote a grade.

In short, 

90° (or 1 right angle)  =  100^g (100 grades)

1^g (or 1 grade)  =  100' (or 100 minutes)

1' (or 1 minute)  =  100" (or 100 seconds)

Note : 

(i) It is clear that minutes and seconds in sexagesimal and centesimal systems are different.

(iii) Circular System or Radian Measure :

In the circular system , the radian measure of an angle is introduced using arc lengths in a circle of radius r. Circular system is used in all branches of Mathematics and in other applications in Science.

The symbol 1^c is used to denote 1 radian measure.

Radian Measure

The radian measure of an angle is the ratio of the arc length it subtends, to the radius of the circle in which it is the central angle.

Consider a circle of radius r. Let s be the arc length subtending an angle θ at the centre.

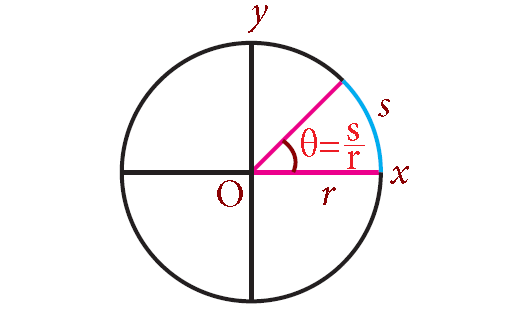
Then, 

θ  =  arc length/radius  =  s/r radians

Hence,

s  =  rθ 

Relationship between Degree and Radian Measures

We have degree and radian units to measure angles. One measuring unit is better than another if it can be defined in a simpler and more intuitive way.

For example, in measuring temperature, Celsius unit is better than Fahrenheit as Celsius was defined using 0° and 100° for freezing and boiling points of water.

Radian measure is better for conversion and calculations. Radian measure is more convenient for analysis whereas degree measure of an angle is more convenient to communicate the concept between people.

Greek Mathematicians observed the relation of π which arises from circumference of a circle and thus, π plays a crucial role in radian measure.

In unit circle, a full rotation corresponds to 360° whereas, a full rotation is related to 2π radians, the circumference of the unit circle.

Thus, we have the following relations :

2π radians  =  360°

Divide each side by 2. 

π radians  =  180° 

Then, 

1 radian  =  (180/π)°  or  1°  =  (π/180) radians

x radians  =  (180x/π)°  or  x°  =  (πx/180) radians

Observe that the scale used in radians is much smaller than the scale in degrees. The smaller scale makes the graphs of trigonometric functions more visible and usable. The above relation gives a way to convert radians into degrees or degrees into radians.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.