SYSTEMS OF LINEAR EQUATIONS WORD PROBLEMS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
A person has $8.80 in pennies and nickels. If there are twice as many nickels as pennies, how many pennies does does the person have?, how many nickels?
Problem 2 :
A total of 78 seats for a concert are sold, producing a total revenue of $483. If seats cost either $2.50 or $10.50, how many $2.50 seats and how many $10.50 seats were sold?
Problem 3 :
Jacob has some 32-cent stamps, some 29-cent stamps, and some 3-cent stamps. The number of 3-cent stamps is 5 less than the number of 29-cent stamps, while the number of 29-cent stamps is 10 less than the number of 32-cent stamps. The total value of the stamps is $9.45. How many of each stamp does he have?
Problem 4 :
Peterson mixes candy that sells for $2.00 per pound with candy that costs $3.60 per pound to make 50 pounds of candy selling for $2.16 per pound. How many pounds of each kind of candy did he use in the mix?
Problem 5 :
Jonathan mixes an alloy containing 14% silver with an alloy containing 24% silver to make 100 pounds of an alloy with 18% silver. How many pounds of each kind of alloy did he use?

Answers
1. Answer :
In this kind of problem, it’s good to do everything in cents to avoid having to work with decimals. So the person has 880 cents total.
Let p be the number of pennies and n be the number of nickels.
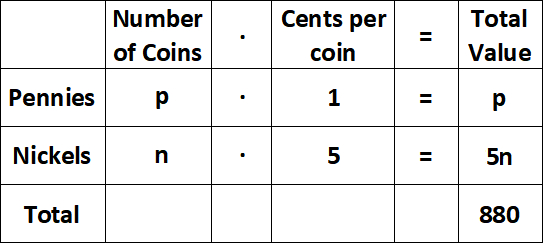
The total value of the coins (880) is the value of the pennies plus the value of the nickels.
From the last column of the table, we have
p + 5n = 880 ----(1)
It is given that there are twice as many nickels as pennies.
n = 2p ----(2)
Substitute n = 2p into (1).
p + 5(2p) = 880
p + 10p = 880
11p = 880
Divide both sides by 11.
p = 80
Substitute p = 80 into (2).
n = 2(80)
n = 160
The person has 80 pennies and 160 nickels.
2. Answer :
Let x be the number $2.50 seats and y be the number of $10.50 seats.
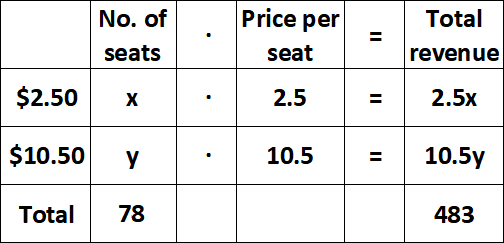
From the second and last columns of the table, we have
x + y = 78 ----(1)
2.5x + 10.5y = 483 ----(2)
Multiply (2) 10 to clear decimals.
10(2.5x + 10.5y) = 10(483)
10(2.5x) + 10(10.5y) = 4830
25x + 105y = 4830
Divide both sides by 5.
5x + 21y = 966 ----(3)
Multiply (1) by -5.
-5(x + y) = -5(78)
-5x + -5y = -390 ----(4)
Add (3) and (4) :
(5x + 21y) + (-5x - 5y) = 966 + (-390)
5x + 21y - 5x - 5y = 966 - 390
16y = 576
Divide each side by 16.
y = 36
Substitute y = 36 into (1).
x + 36 = 78
Subtract 36 from both sides.
x = 42
There were 42 numbers $2.50 seats and 36 numbers of $10.50 seats sold.
3. Answer :
Let x be the number of 32-cent stamps, y be the number of 29-cent stamps and z be the number of 3-cent stamps.
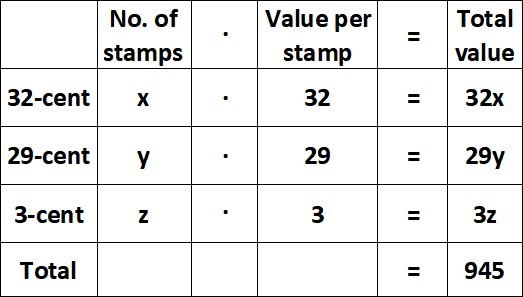
From the last column of the table, we have
32x + 29y + 3z = 945 ----(1)
Given : The number of 3-cent stamps is 5 less than the number of 29-cent stamps, so
z = y - 5 ----(2)
Given : The number of 29-cent stamps is 10 less than the number of 32-cent stamps, so
y = x - 10
x = y + 10 ----(3)
Substitute x = y + 10 and z = y - 5 into (1).
32(y + 10) + 29y + 3(y - 5) = 945
32y + 320 + 29y + 3y - 15 = 945
64y + 305 = 945
Subtract 305 from both sides.
64y = 640
Divide both sides by 64.
y = 10
Substitute y = 10 into (2).
z = 10 - 5
z = 5
Substitute y = 10 into (3).
x = 10 + 10
x = 20
Jacob has 20 numbers of 32-cent stamps, 10 numbers of 29-cent stamps, and 5 numbers 3-cent stamps.
4. Answer :
Let x be the number of pounds of $2 candy and y be the number of pounds of $3.60 candy.
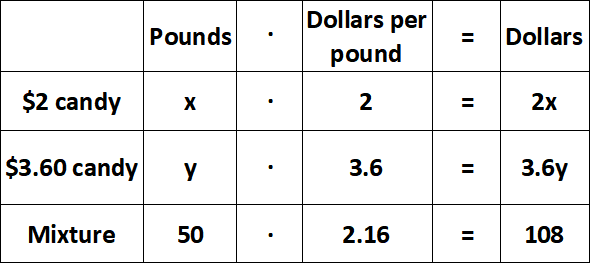
From the second and last columns of the table, we have
x + y = 50 ----(1)
2x + 3.6y = 108 ----(2)
Multiply (2) by 10 to clear decimals.
10(2x + 3.6y) = 10(108)
10(2x) + 10(3.6y) = 1080
20x + 36y = 1080
Divide both sides by 4.
5x + 9y = 270 ----(3)
Multiply (1) by -5.
-5(x + y) = =5(50)
-5x - 5y = -250 ----(4)
Add (3) and (4) :
(5x + 9y) + (-5x - 5y) = 270 + (-250)
5x + 9y - 5x - 5y = 270 - 250
4y = 20
Divide both sides by 5.
y = 5
Substitute y = 5 into (1).
x + 5 = 50
Subtract 5 from both sides.
x = 45
Peterson mixed 45 pounds of the $2 candy and 5 pounds of the $3.60 candy.
5. Answer :
Let x be the number of pounds of 14% alloy and y be the number of pounds of 24% alloy.
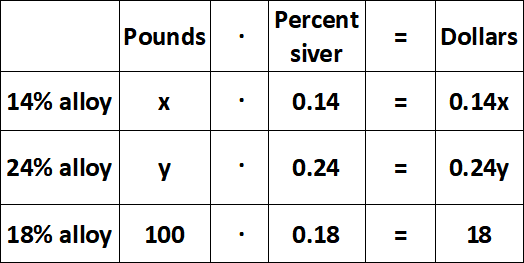
From the second and last columns of the table, we have
x + y = 100 ----(1)
0.14x + 0.24y = 18 ----(2)
Multiply (2) by 100 to clear decimals.
100(0.14x + 0.24y) = 100(18)
100(0.14x) + 100(0.24y) = 1800
14x + 24y = 1800
Divide both sides by 2.
7x + 12y = 900 ----(3)
Multiply (1) by -7.
-7(x + y) = -7(100)
-7x - 7y = -700 ----(4)
Add (3) and (4) :
(7x + 12y) + (-7x - 7y) = 1800 + (-700)
7x + 12y - 7x - 7y = 1800 - 700
5y = 1100
Divide each side by 5 :
y = 40
Substitute y = 40 into (1).
x + 40 = 100
Subtract 40 from both sides.
x = 60
Jonathan mixed 60 pounds of the 14% alloy and 40 pounds of the 24% alloy.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 18, 26 06:52 PM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
