SYSTEM OF LINEAR EQUATIONS IN TWO VARIABLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A linear system of two equations with two variables is any system that can be written in the form.
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
A solution to a system of equations is a value of x and and value of y, when substituted into the equations, satisfies both equations at the same time.
For the example,
3x - y = 7 ----(1)
2x + 3y = 1 ----(2)
3(1) + (2)
9x - 3y + 2x + 3y = 21 + 2
11x = 22
x = 2
By applying the value of x in (1), we get
3(2) - y = 7
6 - y = 7
y = -1
x = 2 and y = −1 is a solution to the system.
Checking :
3x - y = 7 ----(1)
2x + 3y = 1 ----(2)
|
x = 2 and y = -1 3x - y = 7 3(2) - (-1) = 7 6 + 1 = 7 7 = 7 |
x = 2 and y = -1 2x + 3y = 1 2(2) + 3(-1) = 1 4 - 3 = 1 1 = 1 |
The following method are used to solve system of linear equations
(i) Graphing
(ii) Substitution
(iii) Elimination
(iv) Cross multiplication
Example Problem of Solving System of Linear Equations By Graphing Method
Example 1 :
x + y = 7
x - y = 3
Solution :
x + y = 7 ----(1)
x - y = 3 ----(2)
From (1),
y = 7 - x
Substitute some random values for x and solve for y.
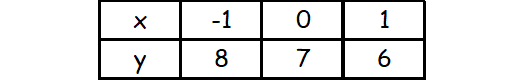
The points on the first line are
(-1, 8), (0, 7), (1, 6)
From (2),
y = x - 3
Substitute some random values for x and solve for y.
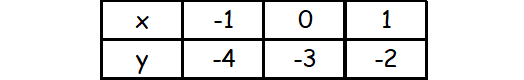
The points on the second line are
(-1, -4), (0, -3), (1, -2)
Plot the points from the above tables and sketch the graph
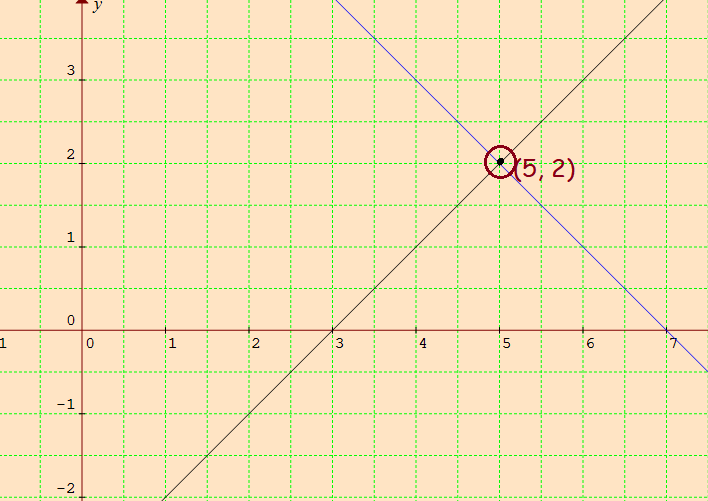
The point of intersection of the two lines is the solution.
So, the solution is (x, y) = (5, 2).
Example Problem of Solving System of Linear Equations By Substitution Method
Example 2 :
Solve the following system of equations by substitution method.
2x - 3y = -1
y = x - 1
Solution :
2x - 3y = -1 ----(1)
y = x - 1 ----(2)
Step 1 :
From (2), substitute (x - 1) for y into (1).
(1)----> 2x - 3(x - 1) = -1
Simplify.
2x - 3x + 3 = -1
-x - 3 = -1
Add 3 to each side.
-x = 2
Multiply each side (-1).
x = -2
Step 2 :
Substitute -2 for x into (2).
(2)----> y = 2 - 1
y = 1
Therefore, the solution is
(x, y) = (-2, 1)
Example Problem of Solving System of Linear Equations By Elimination Method
Example 3 :
Solve the following system of linear equations by elimination method.
x + 2y = 7
x – 2y = 1
Solution :
x + 2y = 7 ----(1)
x – 2y = 1 ----(2)
The coefficients of x and y are equal in both the equations.
(1) + (2) :
2x = 8
x = 8/2
x = 4
By substituting x = 4 in (1), we get
4 + 2y = 7
2y = 7 – 4
2y = 3
y = 3/2
Hence the solution is (4, 3/2).
Example Problem of Solving System of Linear Equations By Cross Multiplication Method
Example 4 :
Solve the following system of linear equations by cross multiplication method.
3x + 4y = 24
20x - 11y = 47
Solution :
3x + 4y - 24 = 0 ----(1)
20x - 11y - 47 = 0 ----(2)
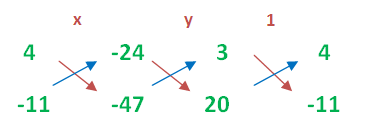
x/(-188 - 264) = y/(-480 -(-141)) = 1/(-33 - 80)
x/(-452) = y/(-480 + 141)) = 1/(-33 - 80)
x/(-452) = y/(-339) = 1/(-113)
|
x/(-452) = 1/(-113) x = 4 |
x/(-339) = 1/(-113) x = 3 |
So, the solution is (4, 3).
Finding Unknown When Solution of Linear Equation is Given
Example 5 :
If the point (4,-2) lies on the line 5x + 2y + k = 0.
Find the value of k.
Solution :
Here the given point (4,-2) lies on the given line.
To solve this problem we have to apply the given points in the equation as the value of x and y.
Here x = 4 and y = -2
The given equation is 5x + 2y + k = 0.
By applying the values of x and y, we get
5(4) + 2(-2) + k = 0
20 - 4 + k = 0
16 + k = 0
k = -16
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

