SYNTHETIC DIVISION
Synthetic division is the method that can be used to divide polynomials. The advantage of this method is that it allows one to calculate without writing variables, than long division.
To use this method in polynomial division, the divisor must be of first degree.
Example 1 :
Find the quotient and remainder when
p(x) = 3x3 - 2x2 - 5 + 7x
is divided by d(x) = x + 3.
Solution :
Step 1 :
Arrange dividend and the divisor in standard form.
Then,
3x3 - 2x2 + 7x - 5 (standard form of dividend)
x + 3 (standard form of divisor)
Write the coefficients of dividend in the first row.
Put ‘0’ for missing term(s).
3 -2 7 -5 (first row)
Step 2 :
Find out the zero of the divisor.
x + 3 = 0
x = -3
Step 3 :
Write the zero of divisor in front of dividend in the first row.
Put ‘0’ in the first column of second row.

Step 4 :
Complete the second row and third row as shown below.
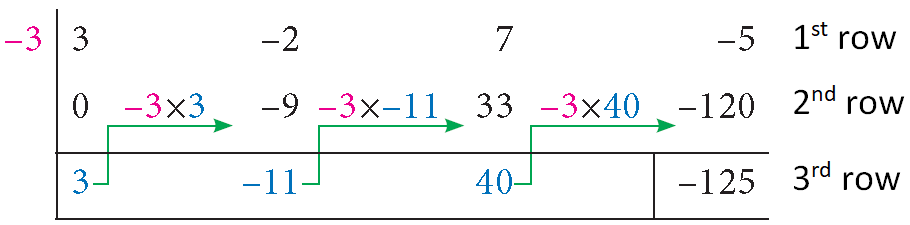
All the entries except the last one in the third row are the coefficients of the quotient.
Therefore, the quotient is
3x2 - 11x + 40
and the remainder is
-125
Example 2 :
Find the quotient and remainder :
(x3 + x2 - 3x + 5) ÷ (x - 1)
Solution :
Arrange dividend and the divisor in standard form.
Then,
x3 + x2 - 3x + 5 (standard form of dividend)
x - 1 (standard form of divisor)
Find out the zero of the divisor.
x - 1 = 0
x = 1
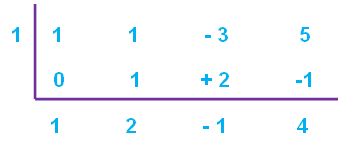
Therefore, the quotient is
x2 + 2x - 1
and the remainder is
4
Example 3 :
Find the quotient and remainder :
(3x3 - 2x2 + 7x - 5) ÷ (x + 3)
Solution :
Arrange dividend and the divisor in standard form.
Then,
3x3 - 2x2 + 7x - 5 (standard form of dividend)
x + 3 (standard form of divisor)
Find out the zero of the divisor.
x + 3 = 0
x = -3
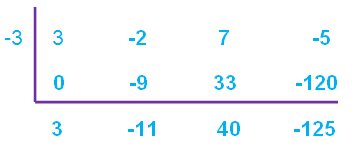
Therefore, the quotient is
3x2 - 11x + 40
and the remainder is
-125
Example 4 :
Find the quotient and remainder :
(3x3 + 4x2 - 10x + 6) ÷ (3x - 2)
Solution :
Arrange dividend and the divisor in standard form.
Then,
3x3 + 4x2 - 10x + 6 (standard form of dividend)
3x - 2 (standard form of divisor)
Find out the zero of the divisor.
3x - 2 = 0
x = 2/3
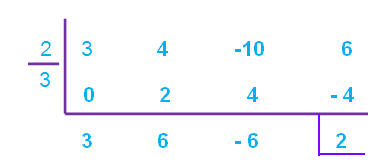
Therefore, the quotient is
3x2 + 6x - 6
and the remainder is
2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
