SURFACE AREA OF SPHERE AND HEMISPHERE

Sphere :

A sphere is the locus of points in space that are a given distance from a point. The point is called the center of the sphere. A radius of a sphere is a segment from the center to a point on the sphere.

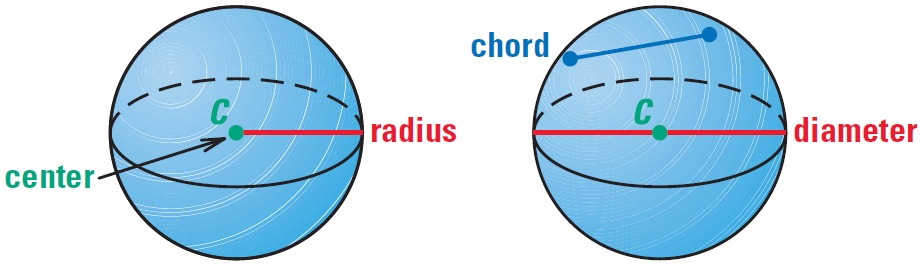
A chord of a sphere is a segment whose endpoints are on the sphere. A diameter is a chord that contains the center. As with circles, the terms radius and diameter also represent distances, and the diameter is twice the radius.

Hemisphere :

Curved surface area   =  3Πr²

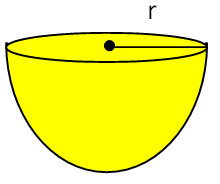
Curved surface area   =  2Πr²

Total surface area of  =  3Πr²

Hollow hemisphere :

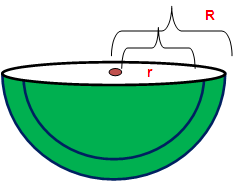
Hollow hemisphere  =  2Π(R² + r²) sq. units

Hollow hemisphere  =  Π(3R² + r²) sq. units

Example 1 :

If the curved surface area of solid sphere is 98.56 cm², then find the radius of the sphere.

Solution :

Curved surface area of sphere  =  98.56 cm²

4 Π r²  =  98.56

4 ⋅ (22/7) ⋅ r²  = 98.56

r²  =  98.56 ⋅ (1/4) ⋅ (7/22)

r²  =  98.56 ⋅ (1/4) ⋅ (7/22)

r²  =  7.84

r  =  √(2.8 ⋅ 2.8) 

r  =  2.8 cm

So, radius of the sphere is 2.8 cm.

Example 2 :

If the curved surface area of the solid hemisphere is 2772 sq.cm, then find its total surface area.

Solution  :

Curved surface area of hemisphere  =  2772 cm²

2Πr²  =  2772

2 ⋅ (22/7) ⋅ r²  =  2772

r²  =  2772 ⋅ (1/2) ⋅ (7/22)

r²  =  441

r  =  21

Total surface area of hemisphere  =  3Πr²

=  3 ⋅ (22/7) ⋅(21)²

=  4158 cm² 

Total surface area of sphere = 4158 cm²  

Example 3 :

Radii of two solid hemispheres are in the ratio 3:5. Find the ratio of their curved surface areas and the ratio of their total surface areas.

Solution :

Let r₁ and r₂ are the radii of two hemispheres

r₁ : r₂  =  3:5

r₁ / r₂  =  3/5

r₁  =  3r₂/5

Curved surface area of hemisphere  =  2Πr²

Ratio of curved surface area of two hemisphere

2 Π r² : 2 Π r²

(3 r₂/5)² : r₂²

9 : 25

Total surface area of hemisphere =  3Πr²

Ratio of curved surface area of two hemisphere

3Π r₁² : 3 Πr₂²

(3 r₂/5)² : r₂²

9 : 25

Ratio of curved surface area is 9 : 25

Ratio of total surface area is 9 : 25

Example 4 :

Find the total surface area of a hemisphere of radius r/2unit.

Solution :

Total surface area of hemisphere = 3Π r²

Here radius (r) = r/2 units

= 3Π (r/2)²

= 3Π r²/4

= 0.75Π r²

So, the required total surface area of hemisphere is 

0.75Π r²

Example 5 :

The entrance to the Civil Rights Institute in Birmingham, Alabama, includes a hemisphere that has a radius of 25.3 feet.

a. Find the volume of the hemisphere.

b. Find the surface area of the hemisphere, not including its base.

c. The walls of the hemisphere are 1.3 feet thick. So, the rounded surface inside the building is a hemisphere with a radius of 24 feet. Find its surface area, not including its base.

Solution :

a)

Volume of hemisphere = (2/3) Π r³

r = 25.3 ft

Volume = (2/3) Π (25.3)³

= 33900.01 cubic ft

b)  

Surface area of the hemisphere = 2 Π r²

= 2(3.14)(25.3)²

= 4019.75 square ft

c)  Surface area of the hemisphere inside = 2 Π r²

r = 24 feet

= 2 x 3.14 (24)²

= 3617.28 square ft

Area of the base =  Π (R² - r²)

= 3.14((24+1.3)² - 24²)

= 3.14((25.3)² - 24²)

= 3.14(640.09 - 576)

= 3.14(64.09)

= 201.24 square ft

Total area = 3617.28 + 201.24

= 3818.52 square ft

Example 6 :

The internal and external diameters of hollow hemispherical vessel are 24 cm and 25 cm respectively. If the cost of painting 1cm² surface area is $1.5, find the total cost of painting the vessel all over.

Solution :

Surface area of hemisphere = 2 Π (R - r)

Internal diameter = 24 cm, r = 24/2 ==> 12 cm

External diameter = 25 cm, R = 25/2 ==> 12.5 cm

= 2 x (22/7) (12.5 - 12)

= 2 (3.14) x 0.5

= 3.14 cm²

Cost of painting 1 cm² = $1.5

Total cost = 1.5 (3.14)

= $4.71

So, the required cost is $4.71

Example 7 :

If the base area of a hemispherical solid is 1386 sq. metres, then find its total surface area?

Solution :

Base area of hemisphere = 1386

Π R² = 1386

3.14 R² = 1386

R² = 1386 / 3.14

R² = 441.40

R = 21

So, the radius of the hemisphere = 21 cm

To find total surface area, we use the formula 3Π R²

= 3(3.14) (21)²

= 4154.22 cm²

Example 8 :

The internal and external radii of a hollow hemispherical shell are 3 m and 5 m respectively. Find the C.S.A of the shell.

Solution :

R = 5 m and r = 3 cm

Curved surface area = 2 Π(R² + r²)

= 2 x (3.14) (5² + 3²)

= 6.28 (25 + 9)

= 6.28 x 34

= 213.52 m²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.