SURFACE AREA OF PYRAMIDS AND CONES WORKSHEET

Problem 1 :

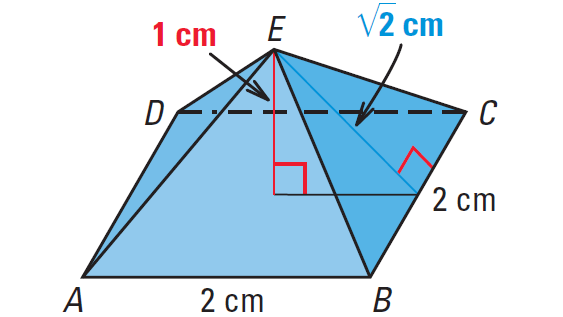
Find the surface area of the regular pyramid shown below. 

Problem 2 :

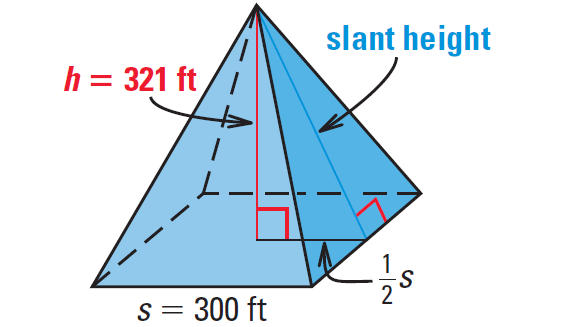
The lateral faces of the Pyramid Arena in Memphis, Tennessee, are covered with steel panels. Use the diagram of the arena shown below to find the area of each lateral face of this regular pyramid.

Problem 3 :

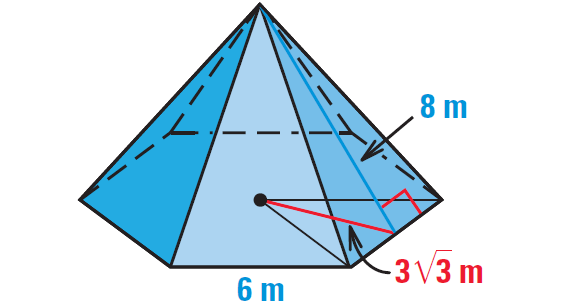
Find the surface area of the regular pyramid shown below. 

Problem 4 :

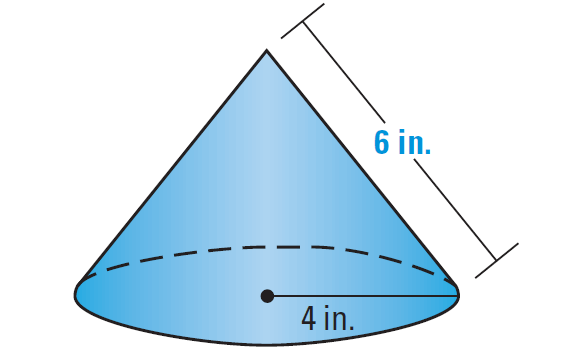
Find the surface area of the right cone shown below. 

Problem 5 :

The surface area of a right cone is 30π square inches and the slant height is 7 inches. Find the radius of the base of the cone.

Answers

1. Answer :

The base is a square.   

Use the formula for the area of a square to find the area of the base,

B  =  side ⋅ side

B  =  2 ⋅ 2

B  =  4 cm²

The perimeter of the base is

P  =  4 ⋅ side

P  =  4 ⋅ 2

P  =  8 cm

The slant height is 

l  =  √2 cm

Formula surface area of a right pyramid is

S  =  B + 1/2 ⋅ Pl

Substitute 4 for the area of the base B, 8 for P and √2 for l.

S  =  4 + 1/2 ⋅ (8)(√2)

Simplify.

S  =  4 + 4√2

Use calculator. 

S  ≈  9.7

So, the surface area of the regular pyramid is about 9.7 square cm. 

2. Answer :

To find the slant height of the pyramid, use the Pythagorean Theorem in the right triangle triangle shown below.

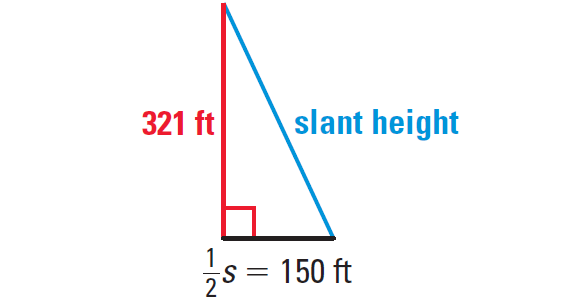
(Slant height)²  =  h² + (1/2 ⋅ s)²

Substitute.

(Slant height)²  =  321² + 150²

Simplify. 

(Slant height)²  =  103,041 + 22,500

(Slant height)²  =  103,041 + 22,500

(Slant height)²  =  125,541

Take square root on both sides. 

(Slant height)²  =  √125,541

Use calculator. 

Slant height  ≈  354.32

The area of each lateral face is

=  1/2 ⋅ (base area of lateral face)(slant height)

Substitute.

≈  1/2 ⋅ (300)(354.32)

≈  53,148

So, the area of each lateral face is about 53,148 square feet.

3. Answer :

To find the surface area of the regular pyramid shown, start by finding the area of the base.

A diagram of the base is shown below. 

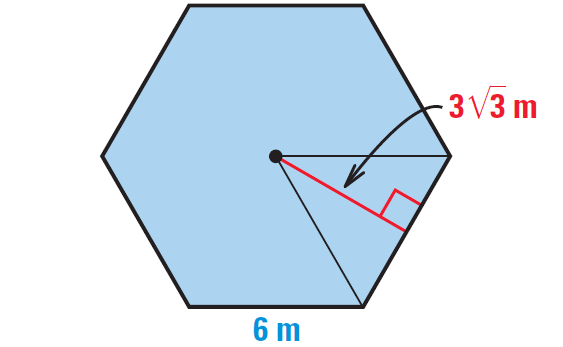
The base is a regular hexagon. 

Use the formula for the area of a regular polygon to find the area of the base,

=  1/2 ⋅ (apothem)(perimeter)

Substitute.

=  1/2 ⋅ (3√3)(6 ⋅ 6)

Simplify.

=  54√3 square meters

Formula for area of a regular pyramid is

S  =  B + 1/2 ⋅ Pl

Substitute 54√3 for the area of the base B, 36 for P and 8 for l. 

S  =  54√3 + 1/2 ⋅ (36)(8)

Simplify.

S  =  54√3 + 144

Use calculator.

S  ≈  237.5

So, the surface area of the regular pyramid is about 237.5 square meters.

4. Answer :

Formula for surface area of a right cone is 

S  =  πr² + πrl

Substitute. 

S  =  π(4²) + π(4)(6)

Simplify.

S  =  16π + 24π

S  =  40π

Use calculator. 

S  ≈  125.7

So, the surface area of the right cone is about 125.7 square inches.

5. Answer :

Formula for surface area of a right cone is 

S  =  πr² + πrl

Substitute.

30π  =  πr² + πr(7)

Factor.

30π  =  π(r² + 7r)

Divide each side by π. 

30  =  r² + 7r

Subtract 30 from each side. 

0  =  r² + 7r - 30

or 

r² + 7r - 30  =  0

Solve the above quadratic equation using factoring 

(r - 3)(r + 7)  =  0

r - 3  =  0     or     r + 7  =  0

r  =  3     or     r  =  -7

Radius can not be negative. Then, r  =  3. 

So, the radius of the base of the cone is 3 inches. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.